
分析 要使得內接△ABP面積最大,則只須使得過P點的切線與直線2x-y+4=0平行,由導數的性質能求出P位于(4,4)點處時,△ABP面積最大.
解答 解:要使得內接△ABP面積最大,則只須使得過P點的切線與直線2x-y+4=0平行,
∵x2=4y,
∴y=$\frac{1}{4}{x}^{2}$,
∵y′=$\frac{1}{2}x$,直線2x-y+4=0斜率為2,
∴過P點的切線斜率k=yp′=2,
解得xP=4,則可得yP=4
∴P位于(4,4)點處時,△ABP面積最大.兩條平行線間的距離為$\frac{4}{\sqrt{5}}$,
直線2x-y+4=0與拋物線x2=4y聯立,可得x2-8x-16=0,
∴|AB|=$\sqrt{1+4}•\sqrt{36+64}$=10$\sqrt{5}$,
∴△ABP面積的最大值是$\frac{1}{2}×10\sqrt{5}×\frac{4}{\sqrt{5}}$=20,
故答案為:20.
點評 本題主要考查拋物線標準方程,簡單幾何性質,直線與拋物線的位置關系等基礎知識.考查運算求解能力,推理論證能力;考查化歸與轉化思想.解題時要認真審題,注意導數性質的靈活運用.


科目:高中數學 來源: 題型:解答題
 PM2.5是指空氣中直徑小于或等于2.5微米的顆粒物(也稱為入肺顆粒物),為了探究車流量與PM2.5的濃度失分相關,現采集某城市周一至周五時間段車流量與PM2.5的數據如表”
PM2.5是指空氣中直徑小于或等于2.5微米的顆粒物(也稱為入肺顆粒物),為了探究車流量與PM2.5的濃度失分相關,現采集某城市周一至周五時間段車流量與PM2.5的數據如表”| 時間 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 車流量x(萬輛) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的濃度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,已知$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$,任意點M關于點A的對稱點為S,點S關于點B的對稱點為N,則$\overrightarrow{MN}$=( )
如圖,已知$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$,任意點M關于點A的對稱點為S,點S關于點B的對稱點為N,則$\overrightarrow{MN}$=( )| A. | $\overrightarrow a+\overrightarrow b$ | B. | $2\overrightarrow a+3\overrightarrow b$ | C. | $3\overrightarrow a-2\overrightarrow b$ | D. | $2\overrightarrow b-2\overrightarrow a$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{π}{6}$,0) | B. | (-$\frac{π}{12}$,$\frac{π}{6}$) | C. | (0,$\frac{π}{6}$) | D. | ($\frac{π}{6}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 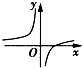 | B. | 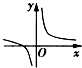 | C. | 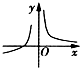 | D. | 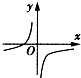 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com