
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
分析 設等比數列{an}的公比為q,且q>0,由題意和等差中項的性質列出方程,由等比數列的通項公式化簡后求出q,由等比數列的通項公式化簡所求的式子,化簡后即可求值.
解答 解:設等比數列{an}的公比為q,且q>0,
∵a3,$\frac{1}{2}{a_5},{a_4}$成等差數列,
∴$2×\frac{1}{2}{a}_{5}={a}_{3}+{a}_{4}$,則${a}_{3}{q}^{2}={a}_{3}+{a}_{3}q$,
化簡得,q2-q-1=0,解得q=$\frac{1±\sqrt{5}}{2}$,
則q=$\frac{\sqrt{5}+1}{2}$,
∴$\frac{{a}_{3}+{a}_{5}}{{a}_{4}+{a}_{6}}$=$\frac{{a}_{3}+{a}_{5}}{{a}_{3}q+{a}_{5}q}$=$\frac{1}{q}$=$\frac{2}{\sqrt{5}+1}$=$\frac{\sqrt{5}-1}{2}$,
故選A.
點評 本題考查等比數列的通項公式,以及等差中項的性質的應用,屬于基礎題.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{10}x±2y=0$ | B. | $2x±\sqrt{10}y=0$ | C. | $\sqrt{6}x±2y=0$ | D. | $2x±\sqrt{6}y=0$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
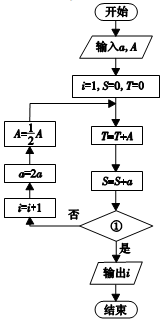 我國古代數學典籍《九章算術》第七章“盈不足”中有一問題:
我國古代數學典籍《九章算術》第七章“盈不足”中有一問題:| A. | T>2S? | B. | S>2T? | C. | S<2T? | D. | T<2S? |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 504 | C. | 1008 | D. | 2016 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com