
分析 根據題意得出k>$\frac{{x}_{0}(l{nx}_{0}+1)}{{x}_{0}-2}$,設f(x)=$\frac{x(lnx+1)}{x-2}$,其中x>2;利用導數求出f(x)在x>2的最小值,即可求出正整數k的最小值.
解答 解:?x0∈(2,+∞),∴x0-2>0,
∴k(x0-2)>x0(lnx0+1)可化為
k>$\frac{{x}_{0}(l{nx}_{0}+1)}{{x}_{0}-2}$,
設f(x)=$\frac{x(lnx+1)}{x-2}$,其中x>2;
則f′(x)=$\frac{[(lnx+1)+1](x-2)-x(lnx+1)}{{(x-2)}^{2}}$=$\frac{x-4-2lnx}{{(x-2)}^{2}}$;
令f′(x)=0,
得x-4-2lnx=0,
設g(x)=x-4-2lnx,其中x>2;
則g′(x)=1-$\frac{2}{x}$=$\frac{x-2}{x}$,
當x>2時,g′(x)>0,g(x)是單調增函數,
∴g(x)≥g(2);
且g(2)=2-4-2ln2=-2-2×0.6931<0,
g(5)=5-4-2ln5=1-2×1.6094<0,
g(8)=8-4-2ln8=4-6ln2=4-6×0.6931<0,
g(9)=9-4-2ln9=5-4ln3=5-4×1.0986>0;
∴g(x)在(8,9)內有零點,
且在零點處f(x)取得最小值m;
∴f(8)=$\frac{8(ln8+1)}{6}$=$\frac{4}{3}$×(3ln2+1)=$\frac{4}{3}$×(3×0.6931+1)≈4.1>m,
f(9)=$\frac{9(ln9+1)}{7}$=$\frac{9}{7}$×(2ln3+1)=$\frac{9}{7}$×(2×1.0986+1)≈4.1>m;
∴k≥4.1;
即正整數k的最小值為5.
故答案為:5.
點評 本題考查了特稱命題的應用問題,也考查了不等式與函數的應用問題,是綜合性題目.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
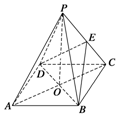 如圖所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面邊長為a,E是PC的中點.
如圖所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面邊長為a,E是PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
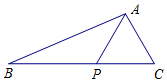 如圖,在△ABC中,點P在BC邊上,∠PAC=60°,PC=2,AP+AC=4.
如圖,在△ABC中,點P在BC邊上,∠PAC=60°,PC=2,AP+AC=4.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8π | B. | 12π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com