Question

5．過雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左焦點F（-c，0）（c＞0）作圓${x^2}+{y^2}=\frac{a^2}{4}$的切線，切點為E，延長FE交雙曲線右支于點P．若$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$，則雙曲線的漸近線方程為（　　）

• A． $\sqrt{10}x±2y=0$
• B． $2x±\sqrt{10}y=0$
• C． $\sqrt{6}x±2y=0$
• D． $2x±\sqrt{6}y=0$

Answer 1

分析 判斷出E為PF的中點，據雙曲線的特點知原點O為兩焦點的中點；利用中位線的性質，求出PF′的長度及判斷出PF′垂直于PF；通過勾股定理得到a，c的關系，再由c²=a²+b²，求出$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$，問題得以解決．

解答 解：∵$\overrightarrow{OP}=2\overrightarrow{OE}-\overrightarrow{OF}$，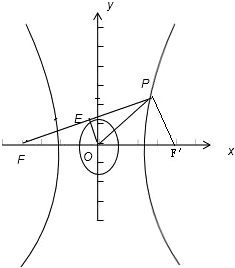
∴$\overrightarrow{OE}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{OF}$）
∴E為PF的中點，令右焦點為F′，則O為FF′的中點，
則PF′=2OE=a，
∵E為切點，
∴OE⊥PF
∴PF′⊥PF
∵PF-PF′=2a
∴PF=PF′+2a=3a
在Rt△PFF′中，PF²+PF′²=FF′²
即9a²+a²=4c²=4（a²+b²），
∴3a²=2b²，
∴$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$，
∴漸近線方程為y=±$\frac{\sqrt{6}}{2}$x，即$\sqrt{6}$x±2y=0，
故選：C

點評 本小題主要考查雙曲線的簡單性質、圓的方程等基礎知識，考查運算求解能力，考查數形結合思想、化歸與轉化思想，在圓錐曲線中，求離心率關鍵就是求三參數a，b，c的關系，屬于中檔題．