
分析 (Ⅰ)由已知利用平面向量數量積的運算可得f(x)=sin($\frac{2x}{3}$+$\frac{π}{6}$)+$\frac{1}{2}$,利用周期公式可求最小正周期,令$\frac{2x}{3}$+$\frac{π}{6}$=kπ,k∈Z,即可解得f(x)的對稱中心.
(Ⅱ)由兩角和的正弦函數公式,三角形內角和定理化簡已知等等可得2sinAcosC=sinA,結合sinA>0,可求cosC=$\frac{1}{2}$,可得C的值,又f(A)=sin($\frac{2A}{3}$+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{3}{2}$,進而解得A的值,利用正弦定理可求c的值.
解答 解:(Ⅰ)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=$\sqrt{3}$sin$\frac{x}{3}$cos$\frac{x}{3}$+cos2$\frac{x}{3}$=$\frac{\sqrt{3}}{2}$sin$\frac{2x}{3}$+$\frac{cos\frac{2x}{3}+1}{2}$=sin($\frac{2x}{3}$+$\frac{π}{6}$)+$\frac{1}{2}$,
∴f(x)的最小正周期為T=$\frac{2π}{\frac{2}{3}}$=3π,
∴令$\frac{2x}{3}$+$\frac{π}{6}$=kπ,k∈Z,解得:x=-$\frac{π}{4}$+$\frac{3}{2}$kπ,k∈Z,
∴f(x)的對稱中心為:(x=-$\frac{π}{4}$+$\frac{3}{2}$kπ,$\frac{1}{2}$)k∈Z.
(Ⅱ)∵a=2,(2a-b)cosC=ccosB,
∴2sinAcosC=sinCcosB+sinBcosC=sinA,
∵sinA>0,
∴cosC=$\frac{1}{2}$,可得C=$\frac{π}{3}$,
又∵f(A)=sin($\frac{2A}{3}$+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{3}{2}$,
∴sin($\frac{2A}{3}$+$\frac{π}{6}$)=1,
∴A=$\frac{π}{2}$,
∵a=2,
∴c=$\frac{a•sinC}{sinA}$=$\sqrt{3}$.
點評 本題主要考查了平面向量數量積的運算,周期公式,兩角和的正弦函數公式,三角形內角和定理,正弦定理以及正弦函數的圖象和性質的綜合應用,考查了轉化思想,屬于基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
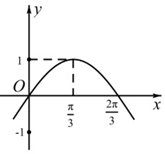 已知函數f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分圖象如圖,則對于區間[0,π]內的任意實數x1,x2,f(x1)-f(x2)的最大值為( )
已知函數f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分圖象如圖,則對于區間[0,π]內的任意實數x1,x2,f(x1)-f(x2)的最大值為( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,三棱柱ABC-A1B1C1的底面是邊長為2正三角形,D是A1C1的中點,且AA1⊥平面ABC,AA1=3.
如圖所示,三棱柱ABC-A1B1C1的底面是邊長為2正三角形,D是A1C1的中點,且AA1⊥平面ABC,AA1=3.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({-∞,\frac{2}{e}})$ | B. | ($\frac{2}{e}$,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com