
分析 (1)由已知條件知,點N是線段FM的中點,NE是線段FM的垂直平分線,點QE的軌跡C是以F為焦點,l為準線的拋物線,寫出拋物線標準方程.
(2)求出P,Q的坐標,可得|PQ|,再換元、配方,即可得出結論.
解答 解:(1)依題意知,NE是線段FM的垂直平分線.
∵ME⊥直線l,∴|EM|是點E到直線l的距離.
∵點E在線段FM的垂直平分線,∴|EM|=|EF|.
故動點E的軌跡C是以F為焦點,l為準線的拋物線,其方程為:y2=8x(x>0).
(2)設A(x1,y1),則OA:y=$\frac{{y}_{1}}{{x}_{1}}$x與y=-4-x聯立,可得P(-$\frac{4{x}_{1}}{{x}_{1}+{y}_{1}}$,-$\frac{4{y}_{1}}{{x}_{1}+{y}_{1}}$),
同理Q(-$\frac{4{x}_{2}}{{x}_{2}+{y}_{2}}$,-$\frac{4{y}_{2}}{{x}_{2}+{y}_{2}}$)
設AB:x=ty+2與拋物線方程聯立,可得y2-8ty-16=0,
∴y1+y2=8t,y1y2=-16
∴|PQ|=$\sqrt{2}$•|x1-x2|=2$\sqrt{2}•|\frac{{y}_{2}-{y}_{1}}{4t+3}|$
=16$\sqrt{2}•\sqrt{\frac{{t}^{2}+1}{(4t+3)^{2}}}$,
令u=4t+3,可得|PQ|=4$\sqrt{2}•\sqrt{25(\frac{1}{u}-\frac{3}{5})^{2}+\frac{16}{25}}$,
∴u=$\frac{5}{3}$,t=-$\frac{1}{3}$時,|PQ|min=$\frac{8\sqrt{2}}{5}$,
x1=2,A(2,4),B(2,-4),P(-$\frac{4}{3}$,-$\frac{8}{3}$),Q(2,-6),
∴|PQ|=$\sqrt{(2+\frac{4}{3})^{2}+(-6+\frac{8}{3})^{2}}$=$\frac{10\sqrt{2}}{3}$$>\frac{8\sqrt{2}}{3}$.
∴線段|PQ|的最小值為$\frac{8\sqrt{2}}{3}$.
點評 本題考查軌跡方程的求法、拋物線的定義、標準方程,以及簡單性質的應用,直線過定點問題,屬于難題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,三棱錐P-ABC中,D,E分別是BC,AC的中點.PB=PC=AB=2,AC=4,BC=2$\sqrt{3}$,PA=$\sqrt{6}$.
如圖,三棱錐P-ABC中,D,E分別是BC,AC的中點.PB=PC=AB=2,AC=4,BC=2$\sqrt{3}$,PA=$\sqrt{6}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
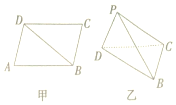 如圖甲,在平行四邊形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,對角線BD=4,現沿對角線BD把△ABD折起,使點A的位置變成點P,且平面PBD⊥平面BCD如圖乙所示,若圖乙中三棱錐P-BCD的四個頂點在同一個球的球面上,則該球的表面積為19π.
如圖甲,在平行四邊形ABCD中,AB=$\sqrt{15}$,AD=$\sqrt{7}$,對角線BD=4,現沿對角線BD把△ABD折起,使點A的位置變成點P,且平面PBD⊥平面BCD如圖乙所示,若圖乙中三棱錐P-BCD的四個頂點在同一個球的球面上,則該球的表面積為19π.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1) | B. | (0,$\frac{1}{3}$) | C. | [$\frac{1}{7}$,$\frac{1}{3}$) | D. | [$\frac{1}{7}$,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com