
分析 (1)分類討論解含參數的不等式;(2)利用遞推式構造新數列$\{\frac{{a}_{n}}{{2}^{n}}\}$是以1為首項,1為公差的等差數列;(3)列項求和,再放縮證明Sn<1.
解答 解:當a=0時,原不等式可化為-x+1<0,即x>1 …(1分)
當a<0時,原不等式可化為(ax-1)(x-1)<0,
即$\b\lc\(\rc\)(\a\vs4\al\co1(x-\frac{1}{a}))$(x-1)>0.因為$\frac{1}{a}$<1,所以x>1或x<$\frac{1}{a}$.…(2分)
當a>0時,不等式可化為$\b\lc\(\rc\)(\a\vs4\al\co1(x-\frac{1}{a}))$(x-1)<0,
①若0<a<1,則$\frac{1}{a}$>1,所以1<x<$\frac{1}{a}$;
②若a=1,則$\frac{1}{a}$=1,不等式無解;
③若a>1,則$\frac{1}{a}$<1,所以$\frac{1}{a}$<x<1.…(4分)
綜上知,當a<0時,原不等式的解集為{x|x<$\frac{1}{a}$或x>1};
當a=0時,原不等式的解集為{x|x>1};
當0<a<1時,原不等式的解集為{x|1<x<$\frac{1}{a}$};
當a=1時,原不等式的解集為∅;
當a>1時,原不等式的解集為{x|$\frac{1}{a}<x<1\}$.…(5分)
(2)∵${a}_{1}=f(2)=2,且f(xy)=xf(y)+yf(x),令x=2,y={2}^{n-1}$ …(6分)
∴f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n…(7分)
即${a}_{n}=2{a}_{n-1}+{2}^{n}(n≥2)$,∴$\frac{{a}_{n}}{{2}^{n}}=\frac{{a}_{n-1}}{{2}^{n-1}}+1$,∴$\{\frac{{a}_{n}}{{2}^{n}}\}$是以1為首項,1為公差的等差數列,
…(8分)
∴$\frac{{a}_{n}}{{2}^{n}}=1+(n-1)=n,即{a}_{n}=n•{2}^{n}$,…(9分)
(3)因為${b}_{n}=\frac{n+2}{n+1}•\frac{1}{{a}_{n}}=2[\frac{1}{n•{2}^{n}}-\frac{1}{(n+1){2}^{n+1}}]$,…(10分)
所以 ${s}_{n}=2[(\frac{1}{1•2}-\frac{1}{2•{2}^{2}})+(\frac{1}{2•{2}^{2}}-\frac{1}{2•{2}^{3}})+…+$$(\frac{1}{n•{2}^{n}}-\frac{1}{(n+1)•{2}^{n+1}})]=2[\frac{1}{2}-\frac{1}{(n+1)•{2}^{n+1}}]<1$ …(12分)
點評 本題考查了分類討論解含參數的不等式、利用遞推式構造新數列及放縮法證明數列不等式,屬于中檔題..


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
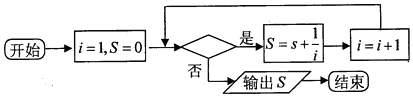
| A. | i≤2014 | B. | i>2014 | C. | i≤2013 | D. | i>2013 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知平面ABB1N⊥平面BB1C1C,四邊形BB1C1C是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.
如圖,已知平面ABB1N⊥平面BB1C1C,四邊形BB1C1C是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com