
分析 (1)由題設條件,得$\overrightarrow{OM}$=(4t2,2t1+4t2),又點M在第二象限或第三象限,列出不等式求出t2的取值范圍;
(2)由平面向量的共線定理,得$\overrightarrow{AM}$=t2$\overrightarrow{AB}$,能證明A,B,M三點共線;
(3)由t1=a2表示出$\overrightarrow{OM}$、$\overrightarrow{AB}$,利用$\overrightarrow{OM}$⊥$\overrightarrow{AB}$求出t2=-$\frac{1}{4}$a2,再由S△ABM=12求出a的值和t2的值.
解答 解:(1)由A(0,2),B(4,6),
得$\overrightarrow{AB}$=(4,4),
∴$\overrightarrow{OM}$=t1$\overrightarrow{OA}$+t2$\overrightarrow{AB}$=(4t2,2t1+4t2),
又點M在第二象限或第三象限,
∴$\left\{\begin{array}{l}{{4t}_{2}<0}\\{{2t}_{1}+{4t}_{2}≠0}\end{array}\right.$,
又t1=2,
解得t2<0且t2≠-1,
∴t2的取值范圍是(-∞,-1)∪(-1,0);
(2)證明:t1=1時,
$\overrightarrow{OM}$=t1$\overrightarrow{OA}$+t2$\overrightarrow{AB}$=$\overrightarrow{OA}$+t2$\overrightarrow{AB}$,
∴$\overrightarrow{OM}$-$\overrightarrow{OA}$=t2$\overrightarrow{AB}$,
即$\overrightarrow{AM}$=t2$\overrightarrow{AB}$,
∴不論t2為何值,A、B、M三點共線;
(3)∵當t1=a2時,$\overrightarrow{OM}$=(4t2,4t2+2a2),
又∵$\overrightarrow{AB}$=(4,4),$\overrightarrow{OM}$⊥$\overrightarrow{AB}$,
∴4t2×4+(4t2+2a2)×4=0,
∴t2=-$\frac{1}{4}$a2.
∴$\overrightarrow{OM}$=(-a2,a2);
又∵|$\overrightarrow{AB}$|=4$\sqrt{2}$,
點M到直線AB:x-y+2=0的距離為
d=$\frac{|{-a}^{2}{-a}^{2}+2|}{\sqrt{2}}$=$\sqrt{2}$|a2-1|;
∵S△ABM=12,
∴$\frac{1}{2}$|$\overrightarrow{AB}$|•d=$\frac{1}{2}$×4$\sqrt{2}$×$\sqrt{2}$|a2-1|=12,
解得a=±2,此時t2=-$\frac{1}{4}$a2=-1.
點評 本題主要考查兩個向量坐標形式的運算,三點共線的條件,兩個向量垂直的性質,點到直線的距離公式的應用問題,是綜合性題目.


 應用題作業本系列答案
應用題作業本系列答案 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,2) | B. | [2,+∞) | C. | (2,+∞) | D. | (-∞,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
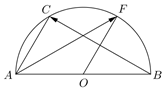 以AB為直徑的半圓,|$\overrightarrow{AB}$|=2,O為圓心,C是$\widehat{AB}$上靠近點A的三等分點,F是$\widehat{AB}$上的某一點,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,則$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.
以AB為直徑的半圓,|$\overrightarrow{AB}$|=2,O為圓心,C是$\widehat{AB}$上靠近點A的三等分點,F是$\widehat{AB}$上的某一點,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,則$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com