
分析 (Ⅰ)由題意可知:b2-b1=a2=-1,b1=b3=1,求得b2=0,代入求得a3=1,根據等差數列的性質,求得d=2,a1=a2-d,即可求得a1的值;
(Ⅱ)由(Ⅰ)可知:an=-3+2(n-1)=2n-5,當n≥2時,bn-bn-1=2n-5,采用“累加法”即可求得bn=n2-4n+4,(n≥2),當n=1時,b1=1也滿足,求得數列{bn}的通項公式.
解答 解:(Ⅰ)由數列{bn}滿足bn-bn-1=an,(n≥2,n∈N*),
∴b2-b1=a2=-1,
b1=b3=1,
∴b2=0,
a3=b3-b2=1,
∵數列{an}是等差數列,
∴d=a3-a2=1-(-1)=2,
∴a1=a2-d=-1-2=-3,
a1的值-3;
(Ⅱ)由(Ⅰ)可知數列{an}是以-3為首項,以2為公差的等差數列,
an=-3+2(n-1)=2n-5,
∴當n≥2時,bn-bn-1=2n-5,
bn-1-bn-2=2(n-2)-5,
…
b2-b1=-1,
將上述等式相加整理得:bn-b1=$\frac{-1+(2n-5)}{2}$•(n-1)=n2-4n+3,
∴bn=n2-4n+4,(n≥2),
當n=1時,b1=1也滿足,
∴bn=n2-4n+4(n∈N*).
點評 本題考查數列的遞推公式,考查等差數列的通項公式的求法,“累加法”求數列的前n項和,考查計算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
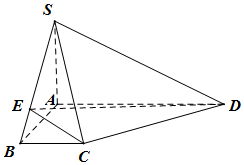 在如圖所示的四棱錐S-ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E為線段BS上的一個動點.
在如圖所示的四棱錐S-ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E為線段BS上的一個動點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com