
| A. | $1或-\frac{1}{3}$ | B. | $\frac{1}{2}或1$ | C. | 1 | D. | $\frac{1}{2}或-\frac{1}{3}$ |
分析 利用函數(shù)的解析式,通過(guò)討論a的范圍,列出方程求解即可.
解答 解:函數(shù)f(x)=$\left\{{\begin{array}{l}{2cosπx,-1<x<0}\\{{e^{2x-1}},x≥0}\end{array}}$滿足f(${\frac{1}{2}}$)+f(a)=2,
當(dāng)a∈(-1,0)時(shí),可得:${e}^{2×\frac{1}{2}-1}$+2cosaπ=2,
可得cosa$π=\frac{1}{2}$,
解得a=$-\frac{1}{3}$.
當(dāng)a>0時(shí),f(${\frac{1}{2}}$)+f(a)=2,
化為:${e}^{2×\frac{1}{2}-1}$+e2a-1=2,
即e2a-1=1,
解得a=$\frac{1}{2}$.
則a的所有可能值為:$\frac{1}{2}或-\frac{1}{3}$.
故選:D.
點(diǎn)評(píng) 本題考查分段函數(shù)的應(yīng)用,函數(shù)零點(diǎn)的個(gè)數(shù)的求法,考查計(jì)算能力.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | {1,2,3} | B. | {1,2} | C. | {1,3} | D. | {2,4} |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 3 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
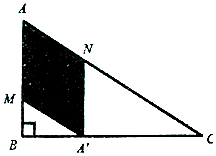 如圖,某小區(qū)準(zhǔn)備將一塊閑置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地開(kāi)發(fā)成公共綠地,設(shè)計(jì)時(shí),要求綠地部分(圖中陰影部分)有公共綠地走道MN,且兩邊是兩個(gè)關(guān)于走道MN對(duì)稱(chēng)的三角形(△AMN和△A′MN),現(xiàn)考慮方便和綠地最大化原則,要求M點(diǎn)與B點(diǎn)不重合,A′點(diǎn)落在邊BC上,設(shè)∠AMN=θ.
如圖,某小區(qū)準(zhǔn)備將一塊閑置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地開(kāi)發(fā)成公共綠地,設(shè)計(jì)時(shí),要求綠地部分(圖中陰影部分)有公共綠地走道MN,且兩邊是兩個(gè)關(guān)于走道MN對(duì)稱(chēng)的三角形(△AMN和△A′MN),現(xiàn)考慮方便和綠地最大化原則,要求M點(diǎn)與B點(diǎn)不重合,A′點(diǎn)落在邊BC上,設(shè)∠AMN=θ.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $y=sin(2x-\frac{π}{6})$,x∈R | B. | $y=sin(\frac{x}{2}+\frac{π}{12})$,x∈R | C. | $y=sin(2x+\frac{π}{6})$,x∈R | D. | $y=sin(2x+\frac{π}{3})$,x∈R |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com