
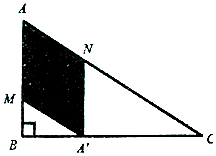
 如圖,某小區準備將一塊閑置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地開發成公共綠地,設計時,要求綠地部分(圖中陰影部分)有公共綠地走道MN,且兩邊是兩個關于走道MN對稱的三角形(△AMN和△A′MN),現考慮方便和綠地最大化原則,要求M點與B點不重合,A′點落在邊BC上,設∠AMN=θ.
如圖,某小區準備將一塊閑置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地開發成公共綠地,設計時,要求綠地部分(圖中陰影部分)有公共綠地走道MN,且兩邊是兩個關于走道MN對稱的三角形(△AMN和△A′MN),現考慮方便和綠地最大化原則,要求M點與B點不重合,A′點落在邊BC上,設∠AMN=θ.分析 由∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a,得∠BAC=$\frac{π}{3}$,設MA=MA′=xa(0<x<1),則MB=a-xa,所以在Rt△MBA′中,cos(π-2θ)=$\frac{a-xa}{xa}$=$\frac{1-x}{x}$;
(1)因為θ=$\frac{π}{3}$,所以cos(π-2θ)=$\frac{1-x}{x}$=$\frac{1}{2}$,解得x值,可得△AMN為等邊三角形,進而得到最美綠地的面積;
(2)根據(1)中結論,可得AN=$\frac{a}{\frac{1}{2}+sin(2θ-\frac{π}{6})}$,根據三角函數的圖象和性質,可得θ=$\frac{π}{3}$時,AN最短,且AN=$\frac{2}{3}a$,進而得到答案.
解答 解:由∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a,得∠BAC=$\frac{π}{3}$…(1分)
設MA=MA′=xa(0<x<1),則MB=a-xa,
所以在Rt△MBA′中,cos(π-2θ)=$\frac{a-xa}{xa}$=$\frac{1-x}{x}$…(3分)
(1)因為θ=$\frac{π}{3}$,所以cos(π-2θ)=$\frac{1-x}{x}$=$\frac{1}{2}$,所以x=$\frac{2}{3}$,
又∠BAC=$\frac{π}{3}$,所以△AMN為等邊三角形,所以綠地的面積S=2×$\frac{1}{2}$×$\frac{2}{3}$a×$\frac{2}{3}$a×sin$\frac{π}{3}$=$\frac{2\sqrt{3}}{9}{a}^{2}$…(5分)
(2)因為cos(π-2θ)═-cos2θ=2sin2θ-1=$\frac{1-x}{x}$,
所以x=$\frac{1}{2{sin}^{2}θ}$,則AM=$\frac{a}{2{sin}^{2}θ}$…(7分)
又∠BAC=$\frac{π}{3}$,所以在△AMN中,∠ANM=$\frac{2π}{3}-θ$,故$\frac{AN}{sinθ}=\frac{AM}{sin(\frac{2π}{3}-θ)}$,
所以AN=$\frac{a}{2{sin}^{2}θ}$×$\frac{sinθ}{sin(\frac{2π}{3}-θ)}$=$\frac{a}{2sinθ•sin(\frac{2π}{3}-θ)}$=$\frac{a}{\frac{1}{2}+sin(2θ-\frac{π}{6})}$…(11分)
又$\frac{π}{4}<θ<\frac{π}{2}$,所以$\frac{π}{3}<2θ-\frac{π}{6}<\frac{5π}{6}$,
所以當$2θ-\frac{π}{6}=\frac{π}{2}$,即θ=$\frac{π}{3}$時,AN最短,且AN=$\frac{2}{3}a$,
此時公共綠地走道MN=$\frac{2}{3}a$…(12分)
點評 本題考查的知識點是函數的應用,函數的最值,熟練掌握三角函數的圖象和性質,是解答的關鍵.


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $1或-\frac{1}{3}$ | B. | $\frac{1}{2}或1$ | C. | 1 | D. | $\frac{1}{2}或-\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A∪B=A | B. | A⊆B | C. | A∩B=∅ | D. | A∩(∁IB)≠∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{13}$ | B. | $\frac{9}{19}$ | C. | $\frac{11}{23}$ | D. | $\frac{9}{23}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com