
| A. | $\sqrt{3}$•f($\frac{π}{6}$)>2cos1•f(1) | B. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) | C. | $\sqrt{6}$f($\frac{π}{6}$)>2f($\frac{π}{4}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>f($\frac{π}{3}$) |
分析 將條件f(x)<f'(x)tanx轉化為$\frac{f'(x)sinx-f(x)cosx}{si{n}^{2}x}$>0,即($\frac{f(x)}{sinx}$)'>0,構造函數g(x)=$\frac{f(x)}{sinx}$,則g(x)在(0,$\frac{π}{2}$)上單調遞增.根據單調性可知,g($\frac{π}{6}$)<g($\frac{π}{3}$),也就是$\frac{f(\frac{π}{6})}{sin\frac{π}{6}}<\frac{f(\frac{π}{3})}{sin\frac{π}{3}}$,即$\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$.
解答 解:∵f(x)<f'(x)tanx,
∴$f(x)<\frac{f'(x)sinx}{cosx}$,
∵$x∈(0,\frac{π}{2})$,∴cosx>0,
∴f'(x)sinx-f(x)cosx>0
記g(x)=$\frac{f(x)}{sinx}$,x$∈(0,\frac{π}{2})$,
則g'(x)=$(\frac{f(x)}{sinx})'=\frac{f'(x)sinx-f(x)cosx}{si{n}^{2}x}>0$,
∴$g(x)在(0,\frac{π}{2})$上單調遞增,
∴$g(\frac{π}{6})<g(\frac{π}{3})$,
∴$\frac{f(\frac{π}{6})}{sin\frac{π}{6}}<\frac{f(\frac{π}{3})}{sin\frac{π}{3}}$,即$\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$.
故選:B.
點評 本題考查了利用導數研究函數的單調性,判斷函數值的大小,將條件進行轉化構造新函數是解決本題的關鍵.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:高中數學 來源: 題型:選擇題
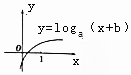 已知函數f(x)=loga(x+b)(a,b為常數)的圖象如圖所示,則函數g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )
已知函數f(x)=loga(x+b)(a,b為常數)的圖象如圖所示,則函數g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )| A. | $\frac{1}{b^4}$ | B. | $\frac{1}{b^5}$ | C. | b4 | D. | b5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 4-$\sqrt{5}$ | D. | 4+$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com