Question

7．F是橢圓$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦點，A（1，1）為橢圓內一定點，P為橢圓上一動點．則|PA|+|PF|的最小值為（　　）

• A． 1
• B． 2
• C． 4-$\sqrt{5}$
• D． 4+$\sqrt{5}$

Answer 1

分析 由題意方程求出兩個焦點的坐標，利用橢圓定義把|PA|+|PF|轉化為2a-（|PF′|-|PA|），數形結合得答案．

解答 解：由$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，得a²=4，b²=3，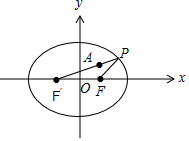
∴$c=\sqrt{{a}^{2}-{b}^{2}}=1$，則橢圓右焦點F（1，0），
左焦點F′（-1，0），
如圖，由橢圓定義得|PF|+|PF′|=2a=4，則|PF|=4-|PF′|，
∴|PA|+|PF|=|PA|+4-|PF′|=4-（|PF′|-|PA|），
連接F′A并延長交橢圓于點P，此時|PF′|-|PA|最大，
最大值為|F′A|=$\sqrt{（-1-1）^{2}+（0-1）^{2}}=\sqrt{5}$，
∴|PA|+|PF|的最小值為4-$\sqrt{5}$．
故選：C．

點評 本題考查直線與橢圓位置關系的應用，考查了橢圓中最值的求法，利用橢圓定義轉化是關鍵，是中檔題．