Question

16．已知函數f（x）=$\left\{\begin{array}{l}-x，x∈[{-1，0}）\\ \frac{1-f（x-1）}{f（x-1）}，x∈[{0，1}）\end{array}\right.$，若方程f（x）-kx+k=0 有二個不同的實數根，則實數k的取值范圍是（　　）

• A． $（{-1，-\frac{1}{2}}]$
• B． $[{-\frac{1}{2}，0}）$
• C． [1，+∞）
• D． $[{-\frac{1}{2}，+∞}）$

Answer 1

分析 先化簡函數的解析式，結合題意可得函數f（x）的圖象和直線y=k（x-1）有2個不同的交點，數形結合求得k的范圍．

解答 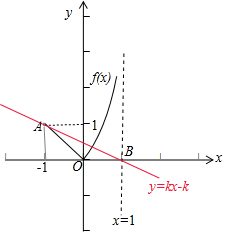解：∵函數f（x）=$\left\{\begin{array}{l}-x，x∈[{-1，0}）\\ \frac{1-f（x-1）}{f（x-1）}，x∈[{0，1}）\end{array}\right.$，
∴當x∈[0，1）時，x-1∈[-1，0），f（x-1）=-（x-1）=1-x，
即f（x）=$\left\{\begin{array}{l}{-x，x∈[-1，0）}\\{\frac{x}{1-x}，x∈[0，1）}\end{array}\right.$．
∵方程f（x）-kx+k=0 有二個不同的實數根，
故函數f（x）的圖象（圖中黑色曲線）和直線y=kx-k（圖中紅色曲線）有2個不同的交點．
如圖所示：
由于直線AB的斜率為$\frac{1-0}{-1-1}$=-$\frac{1}{2}$，故直線y=kx-k的斜率k滿足：0＞k≥-$\frac{1}{2}$，
故選：B．

點評 本題主要考查了方程根的存在性以及個數判斷，體現了數形結合、轉化的數學思想，函數的圖象，屬于中檔題．