
分析 (1)求出函數的導數,解關于導函數的不等式,求出函數的單調區間即可;
(2)問題等價于|f(x1)-f(x2)|max<(6e-2+2)•m恒成立,求出|f(x1)-f(x2)|max,問題轉化為對于任意的a∈(0,2),(6e-2+2)•m>(4+a)e-2+a恒成立,即故m>$\frac{(4+a{)e}^{-2}+a}{{6e}^{-2}+2}$=$\frac{a{(e}^{2}+1)+4}{2{(e}^{2}+3)}$在a∈(0,2)恒成立,從而求出m的范圍即可.
解答 解:(1)當a=1時,f(x)=(x2-x-1)ex,
∴f′(x)=(x2+x-2)ex,
當f′(x)=(x2+x-2)ex>0時,解得x>1或x<-2,函數單調遞增,
當f′(x)=(x2+x-2)ex<0時,解得-2<x<1,函數單調遞減,
∴f(x)在(-∞,-2),(1,+∞)上為增函數,在(-2,1)上為減函數;
(2)a∈(0,2),對于任意x1,x2∈[-4,0],
都有|f(x1)-f(x2)|<(6e-2+2)•m恒成立,
等價于|f(x1)-f(x2)|max<(6e-2+2)•m恒成立,
∵f′(x)=[x2+(2-a)x-2a]ex,
令g(x)=x2+(2-a)x-2a,
△=(2-a)2+8a=(a+2)2≥0,
a=-2時,g(x)=x2+4x+4≥0,
即f′(x)≥0,f(x)在R遞增,
a≠-2時,對于g(x),
△>0,g(x)有2個不相等的實根,
令g(x)=0,解得:x=-2或x=a,
a>-2時,令g′(x)>0,解得:x>a或x<-2,令g(x)<0,解得:-2<x<a,
∴f(x)在(-∞,-2)遞增,在(-2,a)遞減,在(a,+∞)遞增,
∴f(x)在(-4,-2)遞增,在(-2,0)上遞減,
∵f(-2)=(4+a)e-2,f(0)=-a,f(-4)=(16+3a)e-4,
∴|f(x1)-f(x2)|max=f(-2)-f(0)=(4+a)e-2+a,
則問題轉化為對于任意的a∈(0,2),(6e-2+2)•m>(4+a)e-2+a恒成立,
故m>$\frac{(4+a{)e}^{-2}+a}{{6e}^{-2}+2}$=$\frac{a{(e}^{2}+1)+4}{2{(e}^{2}+3)}$在a∈(0,2)恒成立,
而$\frac{a{(e}^{2}+1)+4}{2{(e}^{2}+3)}$<$\frac{2{(e}^{2}+1)+4}{2{(e}^{2}+3)}$=1,
故m≥1.
點評 本題考查了函數的單調性、最值問題,考查導數的由以及轉化思想,是一道中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | f(x)有極值 | B. | f(x)有零點 | C. | f(x)是奇函數 | D. | f(x)是增函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$+$\frac{3}{2}$i | B. | -$\frac{1}{2}$-$\frac{3}{2}$i | C. | -1+3i | D. | -1-3i |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某中學選取20名優秀同學參加2016年數學應用知識競賽,將他們的成績(百分制,均為整數)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],共6組后,得到頻率分布直方圖(如圖),根據圖中的信息,回答下列問題.
某中學選取20名優秀同學參加2016年數學應用知識競賽,將他們的成績(百分制,均為整數)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],共6組后,得到頻率分布直方圖(如圖),根據圖中的信息,回答下列問題.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>b⇒a-c>b-c | B. | a>b⇒ac>bc | C. | a>b⇒a2>b2 | D. | a>b⇒ac2>bc2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
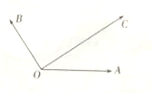 如圖所示,平面內有三個向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$與$\overrightarrow{OC}$的夾角為30°,$\overrightarrow{OB}$與$\overrightarrow{OC}$的夾角為90°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,(λ,μ∈R)則( )
如圖所示,平面內有三個向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$與$\overrightarrow{OC}$的夾角為30°,$\overrightarrow{OB}$與$\overrightarrow{OC}$的夾角為90°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,(λ,μ∈R)則( )| A. | λ=4,μ=2 | B. | λ=4,μ=1 | C. | λ=2,μ=1 | D. | λ=2,μ=2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com