Question

15．某企業生產A、B兩種產品，根據市場調查和預測，A產品的利潤與投資成正比，其關系如圖1，B產品的利潤與投資的算術平方根成正比，其關系如圖2（注：利潤與投資單位是萬元）

（1）分別將A、B兩種產品的利潤表示為投資的函數，并寫出它們的函數關系式；
（2）該企業已籌集到10萬元資金，并全部投入A、B兩種產品的生產，問：怎樣分配這10萬元投資，才能使企業獲得最大利潤，其最大利潤為多少萬元？

Answer 1

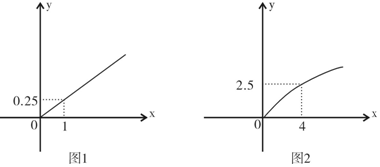
分析 （1）根據函數的模型設出函數解析式，從兩個圖中分別找出特殊點坐標，代入函數解析式求出兩個函數解析式．
（2）將企業獲利表示成對產品B投資x的函數；將函數中的$\sqrt{10-x}$換元為t，將函數轉化為二次函數，求出對稱軸，求出函數的最值．

解答 解：（1）設y=k₁x，由0.25=k₁x₁得：k₁=0.25
設y=k₂$\sqrt{x}$，由2.5=k₂$\sqrt{4}$得k₂=1.25
∴所求函數為y=0.25x及y=1.25$\sqrt{x}$…（4分）
（2）設投入A產品x萬元，則投入B產品為10-x萬元，企業獲得的利潤為y=0.25x+1.25$\sqrt{10-x}$…（6分）
令$\sqrt{10-x}$=t（0≤t≤10）則
y=$\frac{1}{4}$（10-t²）+$\frac{5}{4}$t=$\frac{1}{4}$（-t²+5t+10）
=$\frac{1}{4}$[-（t-$\frac{5}{2}$）²+$\frac{65}{4}$]…（8分）
當t=$\frac{5}{2}$時，y取得最大值$\frac{65}{16}$萬元，此時x=3.75萬元
故對A、B兩種產品分別投資3.75萬元、6.25萬元時，企業可獲得最大利潤$\frac{65}{16}$萬元．…（10分）

點評 本題考查將實際問題的最值問題轉化為函數的最值問題、考查利用待定系數法求函數的解析式、考查換元法注意新變量的范圍、二次函數的最值與對稱軸有關．