Question

4．已知向量$\overrightarrow a=（1，0），\overrightarrow b=（0，1），\overrightarrow c=\overrightarrow a+λ\overrightarrow b（λ∈R）$，向量$\overrightarrow d$如圖表示，則（　　）

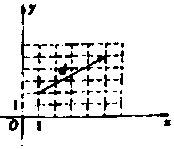
• A． ?λ＞0，使得$\overrightarrow c⊥\overrightarrow d$
• B． ?λ＞0，使得＜$\overrightarrow{c}$，$\overrightarrowp9vv5xb5$＞=60°
• C． ?λ＜0，使得＜$\overrightarrow{c}$，$\overrightarrowp9vv5xb5$＞=30°
• D． ?λ＞0，使得$\overrightarrow c=m\overrightarrow d（m$為不為0的常數）

Answer 1

分析 由題意可得向量$\overrightarrow{c}=\overrightarrow{a}+λ\overrightarrow{b}=（1，λ）$，向由圖可得$\overrightarrowp9vv5xb5$=（5，5）-（1，2）=（4，3）．再對選項逐一判定即可．

解答 解：向量$\overrightarrow{c}=\overrightarrow{a}+λ\overrightarrow{b}=（1，λ）$，向由圖可得$\overrightarrowp9vv5xb5$=（5，5）-（1，2）=（4，3）．
對于A，若$\overrightarrow c⊥\overrightarrow d$，則（1，λ）•（4，3）=0，解得$λ=-\frac{4}{3}＜0$，故錯；
對于B，若＜$\overrightarrow{c}$，$\overrightarrowp9vv5xb5$＞=60°，則$\frac{4+3λ}{5\sqrt{1+{λ}^{2}}}=\frac{1}{2}$，得11λ²+96λ+39=0，方程無解，故錯；
對于C，若＜$\overrightarrow{c}$，$\overrightarrowp9vv5xb5$＞=30°，則$\frac{4+3λ}{5\sqrt{1+{λ}^{2}}}=\frac{\sqrt{3}}{2}$，得39λ²-96λ+11=0，方程無解，故錯；
對于D，若$\overrightarrow c=m\overrightarrow d（m$為不為0的常數），則（1，λ）=c（4，3），解得λ=$\frac{3}{4}＞0$，故正確；
故選：D

點評 本題考查了向量的坐標運算性質、向量共線定理，考查了推理能力與計算能力，屬于基礎題．