
| A. | x1+x2-1>0 | B. | x1+x2-1<0 | C. | x2-x1>0 | D. | x2-x1<0 |
分析 通過分段化簡函數解析式,結合f(x1)=f(x2),作差可得f(x2)-f(1-x1)=f(x1)-f(1-x1).構造函數g(x)=f(x)-f(1-x)(0<x<$\frac{1}{2}$).利用導數可得該函數為定義域上的減函數,得到f(x2)>f(1-x1).再由f(x)=x+$\frac{1}{4x}$在($\frac{1}{2}$,+∞)上為增函數,可得x1+x2-1>0.
解答 解:∵f(x)=e|ln2x|-|x-$\frac{1}{4x}$|=$\left\{\begin{array}{l}{2x-(x-\frac{1}{4x}),x≥\frac{1}{2}}\\{\frac{1}{2x}+(x-\frac{1}{4x}),0<x<\frac{1}{2}}\end{array}\right.$,
∴f(x)=x+$\frac{1}{4x}$(x>0),
∵f(x1)=f(x2)且x1≠x2,
∴不妨設x1<x2,則0<x1<$\frac{1}{2}$<x2.
故1-x1>$\frac{1}{2}$.
∴f(x2)-f(1-x1)=f(x1)-f(1-x1).
設g(x)=f(x)-f(1-x)(0<x<$\frac{1}{2}$).
則g(x)=2x+$\frac{1}{4x}+\frac{1}{4(x-1)}-1$.
g′(x)=$2-\frac{1}{4{x}^{2}}-\frac{1}{4(1-x)^{2}}$<0.
∴g(x)在(0,$\frac{1}{2}$)內為減函數.
得g(x)>g($\frac{1}{2}$)=0,
從而f(x2)-f(1-x1)=f(x1)-f(1-x1)>0.
故f(x2)>f(1-x1).
又f(x)=x+$\frac{1}{4x}$在($\frac{1}{2}$,+∞)上為增函數,
∴x2>1-x1,即x1+x2-1>0.
故選:A.
點評 本題考查函數的零點與方程根的關系,考查數學轉化思想方法,訓練了利用導數研究函數的單調性,是中檔題.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:高中數學 來源: 題型:解答題
| 學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 數學偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | B. | -$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | D. | -$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
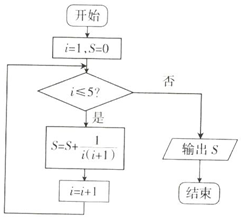
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?λ>0,使得$\overrightarrow c⊥\overrightarrow d$ | B. | ?λ>0,使得<$\overrightarrow{c}$,$\overrightarrowp9vv5xb5$>=60° | ||
| C. | ?λ<0,使得<$\overrightarrow{c}$,$\overrightarrowp9vv5xb5$>=30° | D. | ?λ>0,使得$\overrightarrow c=m\overrightarrow d(m$為不為0的常數) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
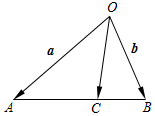 如圖,在△OAB中,C是AB上一點,且AC=2CB,設 $\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\vec b$,則$\overrightarrow{OC}$=$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.(用$\overrightarrow a,\overrightarrow b$表示)
如圖,在△OAB中,C是AB上一點,且AC=2CB,設 $\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\vec b$,則$\overrightarrow{OC}$=$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.(用$\overrightarrow a,\overrightarrow b$表示)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com