
分析 (Ⅰ)由已知數列遞推式可得$8{S_n}={a_n}^2+4{a_n}+4$,進一步得到$8{S}_{n-1}={{a}_{n-1}}^{2}+4{a}_{n-1}+4$(n≥2),兩式作差可得an-an-1-4=0,求出數列首項,代入等差數列通項公式得答案;
(Ⅱ)把{an}的通項公式代入${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,由裂項相消法求數列{bn}的前n項和為Tn.
解答 (Ⅰ)證明:由$\sqrt{2{S_n}}=\frac{{{a_n}+2}}{2}$,得$8{S_n}={a_n}^2+4{a_n}+4$,
∴n≥2時,$8{S}_{n-1}={{a}_{n-1}}^{2}+4{a}_{n-1}+4$(n≥2),
兩式作差得:(an+an-1)(an-an-1-4)=0,
又數列{an}各項為正數,∴an-an-1-4=0,
即數列{an}為等差數列.
又n=1時,$8{S_n}={a_n}^2+4{a_n}+4=8{a_1}$,∴a1=2,
∴通項公式為an=4n-2;
(Ⅱ)∵${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(4n-2)(4n+2)}=\frac{1}{4(2n-1)(2n+1)}=\frac{1}{8}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${T_n}=\frac{1}{8}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…\frac{1}{2n-1}-\frac{1}{2n+1})=\frac{1}{8}(1-\frac{1}{2n+1})$.
點評 本題考查數列遞推式,考查了等差關系的確定,訓練了裂項相消法求數列的前n項和,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
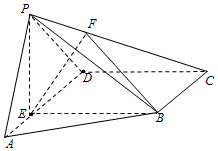 如圖,在四棱錐P-ABCD中,E為AD上一點,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F為PC上一點,且CF=2FP.
如圖,在四棱錐P-ABCD中,E為AD上一點,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F為PC上一點,且CF=2FP.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
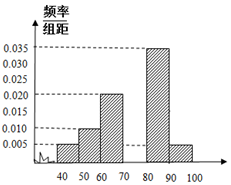 為了估計某校的一次數學考試情況,現從該校參加考試的600名學生中隨機抽出60名學生,其成績(百分制)均在[40,100)上,將這些成績分成六段[40,50),[50,60)…[90,100),后得到如圖所示部分頻率分布直方圖.
為了估計某校的一次數學考試情況,現從該校參加考試的600名學生中隨機抽出60名學生,其成績(百分制)均在[40,100)上,將這些成績分成六段[40,50),[50,60)…[90,100),后得到如圖所示部分頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com