
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 先求出$\overrightarrow{a}$+$\overrightarrow{b}$的坐標,設$\overrightarrow{c}$=(x,y,z),根據(jù)題中的條件求出x+2y+3z=-7,即$\overrightarrow{a}$•$\overrightarrow{c}$=-7,再利用兩個向量的夾角公式,設$\overrightarrow{a}$、$\overrightarrow{c}$ 的夾角等于θ,求出cosθ的值,由此求得θ的值.
解答 解:∵向量$\overrightarrow{a}$=(1,2,3),$\overrightarrow{b}$=(-2,-4,-6),|
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(-1,-2,-3).
設$\overrightarrow{c}$=(x,y,z),
由($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=7,可得 (-1,-2,-3)•(x,y,z)=-x-2y-3y=7,
∴x+2y+3z=-7,即$\overrightarrow{a}$•$\overrightarrow{c}$=-7,
設$\overrightarrow{a}$、$\overrightarrow{c}$ 的夾角等于θ,則cosθ=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}|•|\overrightarrow{c}|}$=$\frac{-7}{\sqrt{1+4+9}•\sqrt{14}}$=-$\frac{1}{2}$.
再由0°≤θ≤180°,可得θ=120°.
故選:C.
點評 本題主要考查兩個向量的夾角公式的應用,求出$\overrightarrow{a}$•$\overrightarrow{c}$=-7是解題的關鍵,屬于中檔題.


 課堂小作業(yè)系列答案
課堂小作業(yè)系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業(yè)本系列答案
名校作業(yè)本系列答案科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\frac{{\sqrt{19}}}{2}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | (2,+∞) | B. | (-∞,2) | C. | (3,+∞) | D. | (-∞,3) |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
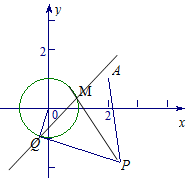 已知圓O:x2+y2=1和定點A(2,1),由圓O外一點P(a,b)向圓O引切線PQ,PM,切點為Q,M,且滿足|PQ|=|PA|.
已知圓O:x2+y2=1和定點A(2,1),由圓O外一點P(a,b)向圓O引切線PQ,PM,切點為Q,M,且滿足|PQ|=|PA|.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com