
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
分析 利用向量的三角形法則和共線定理、平行四邊形法則即可得出.
解答  解:如圖所示,
解:如圖所示,
∵$\overrightarrow{OG}$=$\overrightarrow{OM}$+$\overrightarrow{MG}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{ON}$-$\frac{2}{3}$$\overrightarrow{OM}$=$\frac{1}{6}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$,
又有$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,
∴x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$,
故選:D.
點評 本題考查了向量的三角形法則和共線定理、平行四邊形法則,屬于基礎題.


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案科目:高中數學 來源: 題型:解答題
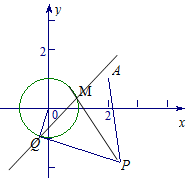 已知圓O:x2+y2=1和定點A(2,1),由圓O外一點P(a,b)向圓O引切線PQ,PM,切點為Q,M,且滿足|PQ|=|PA|.
已知圓O:x2+y2=1和定點A(2,1),由圓O外一點P(a,b)向圓O引切線PQ,PM,切點為Q,M,且滿足|PQ|=|PA|.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
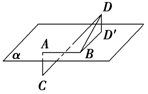 如圖所示,已知線段AB在平面α內,線段AC⊥α,線段BD⊥AB,線段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,則CD的長為2.
如圖所示,已知線段AB在平面α內,線段AC⊥α,線段BD⊥AB,線段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,則CD的長為2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $f({{{log}_3}1.2})>f({-\frac{π}{6}})>f({-1})$ | B. | $f({-\frac{π}{6}})>f({{{log}_3}1.2})>f({-1})$ | ||
| C. | $f({-\frac{π}{6}})>f({-1})>f({{{log}_3}1.2})$ | D. | $f({-1})>f({-\frac{π}{6}})>f({{{log}_3}1.2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com