
| A. | $f({{{log}_3}1.2})>f({-\frac{π}{6}})>f({-1})$ | B. | $f({-\frac{π}{6}})>f({{{log}_3}1.2})>f({-1})$ | ||
| C. | $f({-\frac{π}{6}})>f({-1})>f({{{log}_3}1.2})$ | D. | $f({-1})>f({-\frac{π}{6}})>f({{{log}_3}1.2})$ |
分析 求出函數f(x)的導數,解關于導函數的不等式,求出函數的單調區間,從而求出函數值的大小即可.
解答 解:f(x)=x-2sinx,f′(x)=1-2cosx,
令f′(x)>0,解得:2kπ-$\frac{5π}{3}$<x<2kπ-$\frac{π}{3}$,
令f′(x)<0,解得:2kπ-$\frac{π}{3}$<x<2kπ+$\frac{π}{3}$,
故f(x)在(-$\frac{π}{3}$,$\frac{π}{3}$)遞減,
而-$\frac{π}{3}$<-1<-$\frac{π}{6}$<3log1.2<$\frac{π}{3}$,
故f(-1)>f(-$\frac{π}{6}$)>f(log31.2),
故選:D.
點評 本題考查了函數的單調性問題,考查導數的應用以及三角函數問題,是一道中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
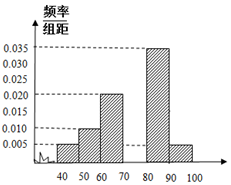 為了估計某校的一次數學考試情況,現從該校參加考試的600名學生中隨機抽出60名學生,其成績(百分制)均在[40,100)上,將這些成績分成六段[40,50),[50,60)…[90,100),后得到如圖所示部分頻率分布直方圖.
為了估計某校的一次數學考試情況,現從該校參加考試的600名學生中隨機抽出60名學生,其成績(百分制)均在[40,100)上,將這些成績分成六段[40,50),[50,60)…[90,100),后得到如圖所示部分頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,+∞) | B. | (1,+∞) | C. | (-2,1) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1) | B. | (-3,0) | C. | (-2,0) | D. | (-1,0) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com