
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{21}}{3}$ | D. | $\frac{\sqrt{3}}{3}$或$\frac{\sqrt{21}}{3}$ |
分析 由等比中項的概念列式求得m值,然后分m=4和m=-4求得圓錐曲線的離心率.
解答 解:∵m是2和8的等比中項,
∴m2=16,得m=±4.
若m=4,則圓錐曲線方程為$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1$,表示焦點在y軸上的橢圓,
此時a=2,c=$\sqrt{{a}^{2}-{b}^{2}}=1$,橢圓離心率為e=$\frac{c}{a}=\frac{1}{2}$;
若m=-4,則圓錐曲線方程為$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{4}=1$,表示焦點在x軸上的雙曲線,
此時a=$\sqrt{3}$,c=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{7}$,雙曲線離心率e=$\frac{\sqrt{7}}{\sqrt{3}}=\frac{\sqrt{21}}{3}$.
∴圓錐曲線$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1的離心率是$\frac{1}{2}$或$\frac{\sqrt{21}}{3}$.
故選:C.
點評 本題考查橢圓與雙曲線的標準方程,考查橢圓與雙曲線的簡單性質,是基礎的計算題.


科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $8+2\sqrt{5}$ | B. | $6+2\sqrt{5}$ | C. | $8+2\sqrt{3}$ | D. | $6+2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD的一個側面PAD為等邊三角形,且平面PAD⊥平面ABCD,四邊形ABCD是平行四邊形,AD=2,AB=4,BD=2$\sqrt{3}$
如圖,四棱錐P-ABCD的一個側面PAD為等邊三角形,且平面PAD⊥平面ABCD,四邊形ABCD是平行四邊形,AD=2,AB=4,BD=2$\sqrt{3}$查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
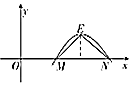 已知奇函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的導函數的部分圖象如圖所示,E是最高點,且△MNE是邊長為1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的導函數的部分圖象如圖所示,E是最高點,且△MNE是邊長為1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com