
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() 且
且![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.

(1)求證:![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析;(2)見解析;(3)![]() .
.
【解析】試題分析:(Ⅰ)利用三角形的中位線得出OM∥VB,利用線面平行的判定定理證明VB∥平面MOC;(Ⅱ)證明OC⊥平面VAB,即可證明平面MOC⊥平面VAB;(Ⅲ)利用等體積法求三棱錐A-MOC的體積即可
試題解析:(Ⅰ)證明:∵O,M分別為AB,VA的中點,
∴OM∥VB,
∵VB平面MOC,OM平面MOC,
∴VB∥平面MOC;
(Ⅱ)證明:∵AC=BC,O為AB的中點,
∴OC⊥AB,
又∵平面VAB⊥平面ABC,平面ABC∩平面VAB=AB,且OC平面ABC,
∴OC⊥平面VAB,
∵OC平面MOC,
∴平面MOC⊥平面VAB
(Ⅲ)在等腰直角三角形![]() 中,
中,![]() ,
,
所以![]() .
.
所以等邊三角形![]() 的面積
的面積![]() .
.
又因為![]() 平面
平面![]() ,
,
所以三棱錐![]() 的體積等于
的體積等于![]() .
.
又因為三棱錐![]() 的體積與三棱錐
的體積與三棱錐![]() 的體積相等,
的體積相等,
所以三棱錐![]() 的體積為
的體積為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】【題目】已知拋物線C:y2=2x,過點(2,0)的直線l交C于A,B兩點,圓M是以線段AB為直徑的圓.
(1)證明:坐標原點O在圓M上;
(2)設圓M過點P(4,-2),求直線l與圓M的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設α,β為兩個不同平面,a,b為兩條不同直線,下列選項正確的是( )
①若a∥α,b∥α,則a∥b
②若aα,α∥β,則a∥β
③若α∥β,a∥β,則![]()
④若a∥α,則a與平面α內的無數條直線平行
⑤若a∥b,則a平行于經過b的所有平面
A.①②B.③④C.②④D.②⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某幾何體的三視圖中,俯視圖是邊長為2的正三角形,正視圖和左視圖分別為直角梯形和直角三角形,則該幾何體的體積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《漢字聽寫大會》不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試.現從某社區居民中隨機抽取50名市民的聽寫測試情況.發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,…,第6組
,…,第6組![]() ,如圖是按上述分組方法得到的頻率分布直方圖.
,如圖是按上述分組方法得到的頻率分布直方圖.

(1)試估計該市市民正確書寫漢字的個數的平均數與中位數;
(2)已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學家歐拉在![]() 年提出定理:三角形的外心、重心、垂心依次位于同一直線上,且重心到外心的距離是重心到垂心距離的一半,這條直線后人稱之為三角形的歐拉線.已知
年提出定理:三角形的外心、重心、垂心依次位于同一直線上,且重心到外心的距離是重心到垂心距離的一半,這條直線后人稱之為三角形的歐拉線.已知![]() 的頂點
的頂點![]() 、
、![]() ,若其歐拉線方程為
,若其歐拉線方程為![]() ,則頂點
,則頂點![]() 的坐標是( )
的坐標是( )
參考公式:若![]() 的頂點
的頂點![]() 、
、![]() 、
、![]() 的坐標分別是
的坐標分別是![]() 、
、![]() 、
、![]() ,則該
,則該![]() 的重心的坐標為
的重心的坐標為![]() .
.
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的函數
上的函數![]() ,有下列說法:
,有下列說法:
(1)函數![]() 滿足
滿足![]() 則函數在
則函數在![]() 上不是單調減函數;
上不是單調減函數;
(2)對任意的![]() 函數
函數![]() 滿足
滿足![]() 則函數在
則函數在![]() 上是單調增函數;
上是單調增函數;
(3)函數![]() 滿足
滿足![]() 則函數
則函數![]() 是偶函數;
是偶函數;
(4)函數![]() 滿足
滿足![]() 則函數
則函數![]() 不是奇函數.
不是奇函數.
其中,正確的說法是________(填寫相應的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水產品經銷商銷售某種鮮魚,售價為每公斤![]() 元,成本為每公斤
元,成本為每公斤![]() 元.銷售宗旨是當天進貨當天銷售.如果當天賣不出去,未售出的全部降價處理完,平均每公斤損失
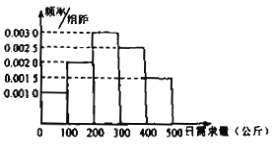
元.銷售宗旨是當天進貨當天銷售.如果當天賣不出去,未售出的全部降價處理完,平均每公斤損失![]() 元.根據以往的銷售情況,按
元.根據以往的銷售情況,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 進行分組,得到如圖所示的頻率分布直方圖.
進行分組,得到如圖所示的頻率分布直方圖.
(1)根據頻率分布直方圖計算該種鮮魚日需求量的平均數![]() (同一組中的數據用該組區間中點值代表);
(同一組中的數據用該組區間中點值代表);
(2)該經銷商某天購進了![]() 公斤這種鮮魚,假設當天的需求量為
公斤這種鮮魚,假設當天的需求量為![]() 公斤
公斤![]() ,利潤為
,利潤為![]() 元.求
元.求![]() 關于
關于![]() 的函數關系式,并結合頻率分布直方圖估計利潤
的函數關系式,并結合頻率分布直方圖估計利潤![]() 不小于
不小于![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com