
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |
分析 分別計算f(0),f(1),f(2),f(e),f(3),f(4),結合零點存在定理,即可得到所求區間.
解答 解:函數f(x)=ln(x+1)-$\frac{1}{x}$在(0,+∞)遞增,
且f(0)不存在,f(1)=ln2-1<0,
f(2)=ln3-$\frac{1}{2}$>0,f(e)=ln(e+1)-$\frac{1}{e}$>0,
f(3)=ln4-$\frac{1}{3}$>0,f(4)=ln5-$\frac{1}{5}$>0,
由零點存在定理可得,
函數f(x)=ln(x+1)-$\frac{1}{x}$的零點所在的大致區間是(1,2).
故選:B.
點評 本題考查函數的零點的范圍,注意運用零點存在定理,考查運算能力,屬于基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
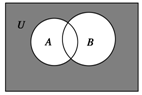 設全集U=R,A={x|y=lg(2x-x2)},B={y|y=cos x},則圖中陰影部分表示的區間是( )
設全集U=R,A={x|y=lg(2x-x2)},B={y|y=cos x},則圖中陰影部分表示的區間是( )| A. | [-1,2) | B. | (-1,2) | C. | (-∞,-1)∪[2,+∞) | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 9 | C. | 4 | D. | 11 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (7,2) | B. | (7,-14) | C. | (7,-4) | D. | (7,-8) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com