
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 通過向量的數(shù)量積的定義,設(shè)出向量的坐標(biāo),利用向量的坐標(biāo)運算和向量的模的公式及幾何意義,結(jié)合圓的方程即可得出最大值為圓的直徑.
解答 解:由平面向量$\overrightarrow{a}$、$\overrightarrow{b}$滿足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,
可得|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=1•1•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,可得<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,
設(shè)$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=(x,y),
則|$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$|≤1,即有|($\frac{1}{2}$+x,y-$\frac{\sqrt{3}}{2}$)|≤1,
即為(x+$\frac{1}{2}$)2+(y-$\frac{\sqrt{3}}{2}$)2≤1,
故|$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$|≤1的幾何意義是在以(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)為圓心,半徑等于1的圓上
和圓內(nèi)部分,
|$\overrightarrow{c}$|的幾何意義是表示向量$\overrightarrow{c}$的終點與原點的距離,而原點在圓上,
則最大值為圓的直徑,即為2.
故選:D.
點評 本題主要考查兩個向量的數(shù)量積的運算,熟練掌握向量的坐標(biāo)運算和圓的方程及數(shù)形結(jié)合是解題的關(guān)鍵,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
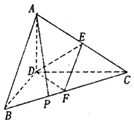 已知三棱錐A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F(xiàn)分別是AC,BC的中點.
已知三棱錐A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F(xiàn)分別是AC,BC的中點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1-1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
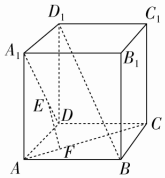 如圖所示,在正方體ABCD-A1B1C1D1中,E、F分別在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,則( )
如圖所示,在正方體ABCD-A1B1C1D1中,E、F分別在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,則( )| A. | EF至多與A1D、AC之一垂直 | B. | EF與A1D、AC都垂直 | ||
| C. | EF與BD1相交 | D. | EF與BD1異面 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com