
分析 (1)設(shè)點(diǎn)M(x,y),利用條件可得等式$\sqrt{(x-1)^{2}+{y}^{2}}$=$\frac{1}{2}$|x-4|,化簡(jiǎn),可得曲線C的軌跡方程;
(2)設(shè)直線l的方程為:x=my+1,A(x1,y1),B(x2,y2).聯(lián)立$\left\{\begin{array}{l}{x=my+1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$得:(4+3m2)y2+6my-9=0.${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}-4}+\frac{{y}_{2}}{{x}_{2}-4}$=$\frac{{y}_{1}({x}_{2}-4)+{y}_{2}({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$=$\frac{2m{y}_{1}{y}_{2}-3({y}_{1}+{y}_{2})}{{m}^{2}{y}_{1}{y}_{2}-3m({y}_{1}+{y}_{2})+9}$
解答 解:(1)設(shè)點(diǎn)M(x,y),則據(jù)題意有$\sqrt{(x-1)^{2}+{y}^{2}}$=$\frac{1}{2}$|x-4|
則4[(x-1)2+y2]=(x-4)2,即3x2+4y2=12,∴$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
曲線C的方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)設(shè)直線l的方程為:x=my+1,A(x1,y1),B(x2,y2).
聯(lián)立$\left\{\begin{array}{l}{x=my+1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$得:(4+3m2)y2+6my-9=0,${y}_{1}{y}_{2}=\frac{-9}{3{m}^{2}+4},{y}_{1}+{y}_{2}=\frac{-6m}{3+4{m}^{2}}$.
${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}-4}+\frac{{y}_{2}}{{x}_{2}-4}$=$\frac{{y}_{1}({x}_{2}-4)+{y}_{2}({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$=$\frac{2m{y}_{1}{y}_{2}-3({y}_{1}+{y}_{2})}{{m}^{2}{y}_{1}{y}_{2}-3m({y}_{1}+{y}_{2})+9}$=0.
k1+k2的值為0
點(diǎn)評(píng) 本題考查了直線與橢圓的位置關(guān)系,屬于中檔題.


 口算題卡加應(yīng)用題集訓(xùn)系列答案
口算題卡加應(yīng)用題集訓(xùn)系列答案 綜合自測(cè)系列答案
綜合自測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
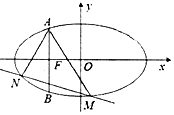 如圖,已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦點(diǎn)F為拋物線y2=-4x的焦點(diǎn),過(guò)點(diǎn)F做x軸的垂線交橢圓于A,B兩點(diǎn),且|AB|=3.
如圖,已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦點(diǎn)F為拋物線y2=-4x的焦點(diǎn),過(guò)點(diǎn)F做x軸的垂線交橢圓于A,B兩點(diǎn),且|AB|=3.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
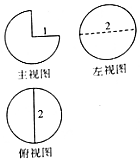
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | π | B. | 3π | C. | 8π | D. | 9π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com