
分析 (1)由題意可得,代值計算即可,
(2)猜想,檢驗n=1時等式成立,假設n=k時命題成立,證明當n=k+1時命題也成立.
解答 解:(1)${b_1}=\frac{3}{4}$,${b_2}=\frac{4}{6}$,${b_3}=\frac{5}{8}$
(2)猜想:${b_n}=\frac{n+2}{2(n+1)}$
①n=1時,${b_1}=\frac{1+2}{4}=\frac{3}{4}$
②假設n=k時,${b_k}=\frac{k+2}{2(k+1)}$
當n=k+1時bk+1=(1-a1)(1-a2)…(1-ak)(1-ak+1)
=bk(1-ak+1)=$\frac{k+2}{2(k+1)}$(1-$\frac{1}{(k+2)^{2}}$)
=$\frac{k+2}{2(k+1)}$•$\frac{{k}^{2}+4k+3}{(k+2)^{2}}$=$\frac{(k+2)(k+1)(k+3)}{2(k+1)(k+2)^{2}}$=$\frac{k+3}{2(k+2)}$
綜合①②:${b_n}=\frac{n+2}{2(n+1)}$.
點評 本題考查數列的遞推公式,用數學歸納法證明等式成立.證明當n=k+1時命題也成立,是解題的難點.


科目:高中數學 來源: 題型:選擇題
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
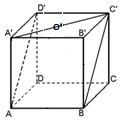 如圖所示,正方體ABCD-A'B'C'D'的棱長為1,點O是正方形A'B'C'D'的中心,則點O到平面ABC'D'的距離是( )
如圖所示,正方體ABCD-A'B'C'D'的棱長為1,點O是正方形A'B'C'D'的中心,則點O到平面ABC'D'的距離是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{13}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{10}{13}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com