
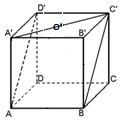
 如圖所示,正方體ABCD-A'B'C'D'的棱長為1,點O是正方形A'B'C'D'的中心,則點O到平面ABC'D'的距離是( )
如圖所示,正方體ABCD-A'B'C'D'的棱長為1,點O是正方形A'B'C'D'的中心,則點O到平面ABC'D'的距離是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
分析 因為O是上底面的中心,O到平面ABC'D'的距離就是A′到平面ABC'D'的距離的一半,就是B′到平面ABC'D'的距離,由此可得結論.
解答  解:因為O是上底面的中心,O到平面ABC'D'的距離就是A′到平面ABC'D'的距離的一半,就是B′到平面ABC'D'的距離,連接B′C,BC′,相交于點O′,則B′C⊥BC′,
解:因為O是上底面的中心,O到平面ABC'D'的距離就是A′到平面ABC'D'的距離的一半,就是B′到平面ABC'D'的距離,連接B′C,BC′,相交于點O′,則B′C⊥BC′,
∵B′C⊥AB,BC′∩AB=B
∴B′C⊥平面ABC'D',
∴B′O′為B′到平面ABC'D'的距離
∵棱長為1,∴B′O′=$\frac{\sqrt{2}}{2}$,
∴點O到平面ABC'D'的距離是:$\frac{\sqrt{2}}{4}$.
故選:D.
點評 本題考查點到面的距離的計算,考查學生分析解決問題的能力,點O到平面ABC'D'的距離轉化為B′到平面ABC'D'的距離是關鍵.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
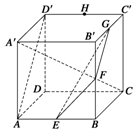 在正方體ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中點分別是E,F,G,H,如圖所示.
在正方體ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中點分別是E,F,G,H,如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -9 | B. | 15 | C. | -15 | D. | ±15 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | i | D. | -i |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com