
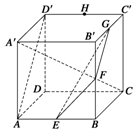
 在正方體ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中點分別是E,F,G,H,如圖所示.
在正方體ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中點分別是E,F,G,H,如圖所示.分析 (1)可通過證明四邊形ABC′D′是平行四邊形,AD′∥BC′得出AD′∥平面EFG;
(2)由A′B′⊥平面BC′可得A′B′⊥BC′,結合BC′⊥B′C得出BC′⊥平面A′B′C,故而A′C⊥BC′,于是A′C⊥FG,同理證出A′C⊥EF,于是A′C⊥平面EFG.
解答 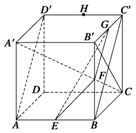 (1)證明 連接BC′.
(1)證明 連接BC′.
在正方體ABCD-A′B′C′D′中,AB=C′D′,AB∥C′D′,
所以四邊形ABC′D′是平行四邊形,
所以AD′∥BC′.
因為F,G分別是BB′,B′C′的中點,
所以FG∥BC′,所以FG∥AD′.
因為EF,AD′是異面直線,所以AD′?平面EFG.
因為FG?平面EFG,所以AD′∥平面EFG.
(2)證明:連接B′C.
在正方體ABCD-A′B′C′D′中,A′B′⊥平面BCC′B′,
BC′?平面BCC′B′,
所以A′B′⊥BC′.
在正方形BCC′B中,B′C⊥BC′,
因為A′B′?平面A′B′C,B′C?平面A′B′C,
A′B′∩B′C=B′,
所以BC′⊥平面A′B′C.
因為A′C?平面A′B′C,所以BC′⊥A′C.
因為FG∥BC′,所以A′C⊥FG,同理可證A′C⊥EF.
因為EF?平面EFG,FG?平面EFG,EF∩FG=F,
所以A′C⊥平面EFG.
點評 本題考查了線面平行與線面垂直的判定,屬于中檔題.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:解答題
 某特色餐館開通了美團外賣服務,在一周內的某特色外賣份數x(份)與收入y(元)之間有如下的對應數據:
某特色餐館開通了美團外賣服務,在一周內的某特色外賣份數x(份)與收入y(元)之間有如下的對應數據:| 外賣份數x(份) | 2 | 4 | 5 | 6 | 8 |
| 收入y(元) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
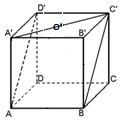 如圖所示,正方體ABCD-A'B'C'D'的棱長為1,點O是正方形A'B'C'D'的中心,則點O到平面ABC'D'的距離是( )
如圖所示,正方體ABCD-A'B'C'D'的棱長為1,點O是正方形A'B'C'D'的中心,則點O到平面ABC'D'的距離是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ②④ | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com