Question

19．如圖（1），五邊形PABCD是由一個正方形與一個等腰三角形拼接而成，其中∠APD=120°，AB=2，現將△PAD進行翻折，使得平面PAD⊥平面ABCD，連接PB，PC，所得四棱錐P-ABCD如圖（2）所示，則四棱錐P-ABCD的外接球的表面積為（　　）

• A． $\frac{14}{3}π$
• B． $\frac{7}{3}π$
• C． $\frac{28}{3}π$
• D． 14π

Answer 1

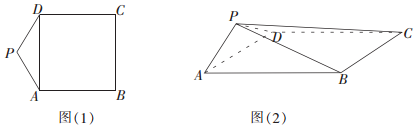
分析 將四棱錐P-ABCD補成直三棱柱PAD-MBC，則直三棱柱PAD-MBC與四棱錐P-ABCD的外接球是同一個球，故只需求出直三棱柱PAD-MBC的外接球半徑即可．

解答 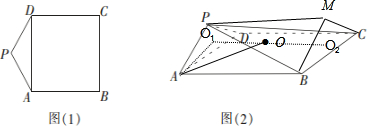解：將四棱錐P-ABCD補成直三棱柱PAD-MBC，
則直三棱柱PAD-MBC與四棱錐P-ABCD的外接球是同一個球，
故只需求出直三棱柱PAD-MBC的外接球半徑即可．
如圖，設直三棱柱PAD-MBC的兩底的外接圓圓心分別為O₁，O₂，連接O₁O₂，
根據對稱性球心為線段O₁O₂的中點O，
又∵底ADP的外接圓半徑r，由正弦定理得$\frac{AD}{sin12{0}^{0}}=2r$，⇒r=$\frac{2}{\sqrt{3}}$，
直三棱柱PAD-MBC的外接球半徑R=$\sqrt{{r}^{2}+O{{O}_{1}}^{2}}=\sqrt{\frac{7}{3}}$．
∴四棱錐P-ABCD的外接球的表面積為s=4πR²=$\frac{28}{3}π$．
故選：C．

點評 本題考查了多面體的外接球，把不易求其外接球半徑的幾何體轉化為易求半徑幾何體，是解題的關鍵，屬于中檔題．