
| A. | 命題“?x∈R,x2-x≤0”的否定是“$?{x_0}∈R,x_0^2-{x_0}≥0$”. | |
| B. | 命題“p∧q為真”是命題“p∨q為真”的必要不充分條件. | |
| C. | “若am2≤bm2,則a≤b”的否命題為真. | |
| D. | 若實數x,y∈[-1,1],則滿足x2+y2≥1的概率為$\frac{π}{4}$. |
分析 A,“≤”的否定是“<”;
B,“p∧q為真”是命題“p∨q為真”的充分不必要條件;
C,am2≤bam2⇒m2>0;
D,∵x2+y2≥1的區域是圓的外面的邊長為2的正方形內的區域,用面積之比即可.
解答 解:對于A,“≤”的否定是“<”,故錯;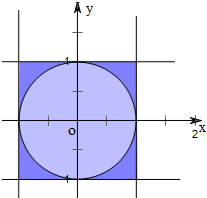
對于B,“p∧q為真”是命題“p∨q為真”的充分不必要條件,故錯;
對于C,am2≤bam2⇒m2>0⇒a≤b,故正確;
對于D,如圖:∵x2+y2≥1的區域是圓的外面的陰影區域,其面積S=4-π,
∴在區間[-1,1]上任取兩個實數x,y,則滿足x2+y2≥1的概率為$\frac{4-π}{4}$.故錯.
故選:C.
點評 本題考查了命題真假的判定,充要條件的判定及幾何概型,屬于中檔題.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{1}{2}$,$\frac{2}{3}$] | B. | ($\frac{1}{2}$,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -a>-b | B. | a+c>b+c | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | (-a)2>(-b)2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
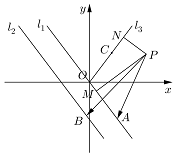 如圖,已知直線l1:kx+y=0和直線l2:kx+y+b=0(b>0),射線OC的一個法向量為$\overrightarrow{n_3}$=(-k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N;
如圖,已知直線l1:kx+y=0和直線l2:kx+y+b=0(b>0),射線OC的一個法向量為$\overrightarrow{n_3}$=(-k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com