Question

12．如圖，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°．BC=CC₁=a，AC=2a．
（1）求證：AB₁⊥BC₁；
（2）求二面角B-AB₁-C的正弦值．

Answer 1

分析 （1）由已知可得AC⊥平面B₁BCC₁，則AC⊥BC₁，再由BC=CC₁，得BC₁⊥B₁C，由線面垂直的判定可得BC₁⊥平面AB₁C，從而得到AB₁⊥BC₁；
（2）設BC₁∩B₁C=O，作OP⊥AB₁于點P，連結BP．由（1）知BO⊥AB₁，進一步得到AB₁⊥平面BOP，說明∠OPB是二面角B-AB₁-C的平面角．然后求解直角三角形得答案．

解答 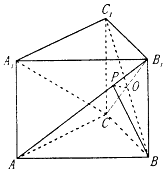（1）證明：∵ABC-A₁B₁C₁是直三棱柱，
∴CC₁⊥平面ABC，則AC⊥CC₁．
又∵AC⊥BC，BC∩CC₁=C，
∴AC⊥平面B₁BCC₁，則AC⊥BC₁，
∵BC=CC₁，∴四邊形B₁BCC₁是正方形，
∴BC₁⊥B₁C，
又AC∩B₁C=C，∴BC₁⊥平面AB₁C，則AB₁⊥BC₁；
（2）解：設BC₁∩B₁C=O，作OP⊥AB₁于點P，連結BP．
由（1）知BO⊥AB₁，而BO∩OP=O，
∴AB₁⊥平面BOP，則BP⊥AB₁，
∴∠OPB是二面角B-AB₁-C的平面角．
∵△OPB₁～△ACB₁，∴$\frac{OP}{AC}=\frac{O{B}_{1}}{A{B}_{1}}$，
∵BC=CC₁=a，AC=2a，∴OP=$\frac{O{B}_{1}•AC}{A{B}_{1}}=\frac{\sqrt{3}}{3}a$，
∴$BP=\sqrt{O{P}^{2}+O{B}^{2}}=\sqrt{（\frac{\sqrt{3}}{3}a）^{2}+（\frac{\sqrt{2}}{2}a）^{2}}$=$\frac{\sqrt{30}}{6}a$．
在Rt△POB中，sin∠OPB=$\frac{OB}{PB}=\frac{\frac{\sqrt{2}}{2}a}{\frac{\sqrt{30}}{6}a}=\frac{\sqrt{15}}{5}$，
∴二面角B-AB₁-C的正弦值為$\frac{\sqrt{15}}{5}$．

點評 本題考查線面垂直的判定和性質，考查空間想象能力和思維能力，訓練了二面角的平面角的求法，是中檔題．