
分析 (1)根據三角形相似得到$\frac{DE}{AD}$=$\frac{BE}{AC}$,得到AE+DE=4,故EA+EB=4是定值,
(2)設出直線方程,聯立方程組,求出x1+1=$\frac{{9k}^{2}-4\sqrt{3}k}{{4k}^{2}+1}$,x2+1=$\frac{{9k}^{2}+4\sqrt{3}k}{{4k}^{2}+1}$,根據y1-y2=k(x1-1)+k(x2-1),求出直線AB的斜率是定值即可.
解答 (1)證明:∵BE∥AC,∴△BDE∽△CAD,
∴$\frac{DE}{AD}$=$\frac{BE}{AC}$,∵AD=AC=4,∴DE=BE,∵AE+DE=4,
故|EA|+|EB|=4是定值,
由橢圓的定義得:$\frac{{x}^{2}}{4}$+y2=1,(y≠0);
(2)解:設A(x1,y1),B(x2,y2),
直線MA的方程是y=k(x-1)+$\frac{\sqrt{3}}{2}$,
直線MB的方程是y=-k(x-1)+$\frac{\sqrt{3}}{2}$,
故$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}{+y}^{2}=1}\\{y=k(x-1)+\frac{\sqrt{3}}{2}}\end{array}\right.$,消去y得:
(4k2+1)x2+(4$\sqrt{3}$k-8k2)x+4k2-4$\sqrt{3}$k-1=0,
x1=1,x2-1=-$\frac{4\sqrt{3}k+2}{{4k}^{2}+1}$,
故y1-y2=k(x1-1)+k(x2-1),
則直線AB的斜率KAB=$\frac{{y}_{2}{-y}_{1}}{{{x}_{2}-x}_{1}}$=$\frac{-4k}{-9\sqrt{3}k}$=$\frac{\sqrt{3}}{6}$.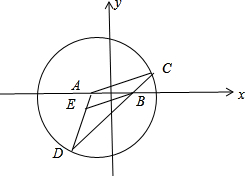
點評 本題考查了直線方程、橢圓的方程問題,考查直線和橢圓的關系,屬于壓軸題.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:高中數學 來源: 題型:解答題
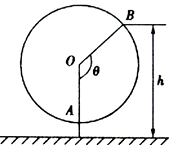 如圖是一個纜車示意圖,該纜車的半徑為4.8m,圓上最低點與地面的距離為0.8m,纜車每60s轉動一圈,圖中OA與地面垂直,以OA為始邊,逆時針轉動θ角到OB,設B點與地面的距離為hm.
如圖是一個纜車示意圖,該纜車的半徑為4.8m,圓上最低點與地面的距離為0.8m,纜車每60s轉動一圈,圖中OA與地面垂直,以OA為始邊,逆時針轉動θ角到OB,設B點與地面的距離為hm.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)有極值 | B. | f(x)有零點 | C. | f(x)是奇函數 | D. | f(x)是增函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$+$\frac{3}{2}$i | B. | -$\frac{1}{2}$-$\frac{3}{2}$i | C. | -1+3i | D. | -1-3i |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某中學選取20名優秀同學參加2016年數學應用知識競賽,將他們的成績(百分制,均為整數)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],共6組后,得到頻率分布直方圖(如圖),根據圖中的信息,回答下列問題.
某中學選取20名優秀同學參加2016年數學應用知識競賽,將他們的成績(百分制,均為整數)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],共6組后,得到頻率分布直方圖(如圖),根據圖中的信息,回答下列問題.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com