
分析 (1)由已知得c=2$\sqrt{3}$,F1(-2$\sqrt{3}$,0),F2(2$\sqrt{3},0$),2a=|AF1|+|AF2|=$\sqrt{(\sqrt{3}+2\sqrt{3})^{2}+(-\frac{\sqrt{13}}{2})^{2}}$+$\sqrt{(\sqrt{3}-2\sqrt{3})^{2}+(-\frac{\sqrt{13}}{2})^{2}}$=8,即可求方程、離心率.
(2)寫出直線TN\TM的方程,得P($\frac{-2{x}_{0}}{{y}_{0}-2},0)$,得Q(0,$\frac{-4{y}_{0}}{{x}_{0}-4}$),即|PN|=|4+$\frac{2{x}_{0}}{{y}_{0}-2}$|=|$\frac{2{x}_{0}+4{y}_{0}-8}{{y}_{0}-2}$|,|MQ|=|2+$\frac{4{y}_{0}}{{x}_{0}-4}$|=|$\frac{2{x}_{0}+4{y}_{0}-8}{{x}_{0}-4}$||PN|•|QM|=$\frac{4({x}_{0}+2{y}_{0}-4)^{2}}{({y}_{0}-2)({x}_{0}-4)}$=$\frac{16({x}_{0}{y}_{0}-2{x}_{0}-4{y}_{0}+8)}{{x}_{0}{y}_{0}-2{x}_{0}-4{y}_{0}+8}=16$.
解答 解:(1)由已知得c=2$\sqrt{3}$,F1(-2$\sqrt{3}$,0),F2(2$\sqrt{3},0$),
∴2a=|AF1|+|AF2|=$\sqrt{(\sqrt{3}+2\sqrt{3})^{2}+(-\frac{\sqrt{13}}{2})^{2}}$+$\sqrt{(\sqrt{3}-2\sqrt{3})^{2}+(-\frac{\sqrt{13}}{2})^{2}}$=8
∴a=4,∴b2=a2-c2=4,e=$\frac{c}{a}=\frac{1}{2}$
橢圓C的標準方程:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$.e=$\frac{1}{2}$.
(2)T(x0,y0),(x0≠0,y0≠0),則$\frac{{{x}_{0}}^{2}}{16}+\frac{{{y}_{0}}^{2}}{4}=1$.
M(0,2),N(4,0),∴直線TM的方程為:$y-2=\frac{{y}_{0}-2}{{x}_{0}}x$,
令y=0,得P($\frac{-2{x}_{0}}{{y}_{0}-2},0)$,
直線TN的方程:$y=\frac{{y}_{0}}{{x}_{0}-4}(x-4)$,
令x=0,得Q(0,$\frac{-4{y}_{0}}{{x}_{0}-4}$)
則|PN|=|4+$\frac{2{x}_{0}}{{y}_{0}-2}$|=|$\frac{2{x}_{0}+4{y}_{0}-8}{{y}_{0}-2}$|
則|MQ|=|2+$\frac{4{y}_{0}}{{x}_{0}-4}$|=|$\frac{2{x}_{0}+4{y}_{0}-8}{{x}_{0}-4}$|
|PN|•|QM|=$\frac{4({x}_{0}+2{y}_{0}-4)^{2}}{({y}_{0}-2)({x}_{0}-4)}$=$\frac{16({x}_{0}{y}_{0}-2{x}_{0}-4{y}_{0}+8)}{{x}_{0}{y}_{0}-2{x}_{0}-4{y}_{0}+8}=16$
∴|PN|•|QM|為定值16
點評 本題考查了橢圓的方程,直線與橢圓的位置關系,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
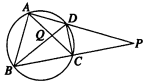 如圖所示,圓內接四邊形ABCD的一組對邊AD,BC的延長線相交于點P,對角線AC,BD相交于點Q,則圖中相似三角形共有( )
如圖所示,圓內接四邊形ABCD的一組對邊AD,BC的延長線相交于點P,對角線AC,BD相交于點Q,則圖中相似三角形共有( )| A. | 4對 | B. | 2對 | C. | 5對 | D. | 3對 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 49% | B. | 53% | C. | 61% | D. | 88% |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
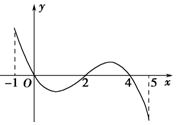 已知函數f(x)的定義域為[-1,5],部分對應值如下表,f(x)的導函數y=f′(x)的圖象如圖所示.下列關于f(x)的命題:
已知函數f(x)的定義域為[-1,5],部分對應值如下表,f(x)的導函數y=f′(x)的圖象如圖所示.下列關于f(x)的命題:| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com