
【題目】已知函數![]() ,若在區間
,若在區間![]() 內有且只有一個實數
內有且只有一個實數![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 在區間
在區間![]() 內具有唯一零點.
內具有唯一零點.
(1)判斷函數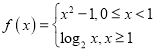 在區間
在區間![]() 內是否具有唯一零點,說明理由:
內是否具有唯一零點,說明理由:
(2)已知向量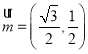 ,
,![]() ,
,![]() ,證明
,證明![]() 在區間
在區間![]() 內具有唯一零點.
內具有唯一零點.
(3)若函數![]() 在區間
在區間![]() 內具有唯一零點,求實數
內具有唯一零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)是,詳見解析(2)證明見解析(3)![]()
【解析】
(1)利用分段函數,分類討論函數的單調性,從而得出結論;
(2)兩個向量的數量積共公式以及三角恒等變換,化簡![]() 的解析式,再利用正弦函數的性質得出結論;
的解析式,再利用正弦函數的性質得出結論;
(3)利用二次函數的性質,分類討論,求得![]() 的范圍.
的范圍.
(1)函數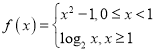 在區間
在區間![]() 內具有唯一零點,理由如下:
內具有唯一零點,理由如下:
當![]() 時,有
時,有![]() ,且當
,且當![]() 時,有
時,有![]() ;
;
當![]() 時,
時,![]() 是增函數,有
是增函數,有![]() ,
,
故函數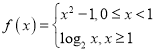 在區間
在區間![]() 內具有唯一零點.
內具有唯一零點.
(2)由向量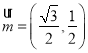 ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
令![]() ,
,![]() ,解得
,解得![]() ,
,
所以函數![]() 在區間
在區間![]() 內具有唯一零點
內具有唯一零點![]() ,使得
,使得![]() ,
,
故函數![]() 在區間
在區間![]() 內具有唯一零點.
內具有唯一零點.
(3)由函數![]() 在區間
在區間![]() 內具有唯一零點,該二次函數的對稱軸為
內具有唯一零點,該二次函數的對稱軸為![]() ,
,
①當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 是增函數,
是增函數,
只需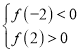 ,即
,即![]() ,解得
,解得![]() ,
,
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
②當![]() ,即
,即![]() 時,若使函數
時,若使函數![]() 在區間
在區間![]() 內具有零點,
內具有零點,
則![]() ,解得
,解得![]() 或
或![]() ,
,
所以,![]() ,
,
i當![]() 時,函數
時,函數![]() 在區間
在區間![]() 內具有唯一零點
內具有唯一零點![]() ,即
,即![]() ,符合題意,
,符合題意,
ii當![]() 時,若使函數
時,若使函數![]() 在區間
在區間![]() 內具有唯一零點,只需
內具有唯一零點,只需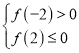 ,
,
即![]() ,解得
,解得![]() ,
,
所以實數![]() 的取值范圍為
的取值范圍為![]() 或
或![]() .
.
③當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 是減函數,
是減函數,
當![]() 時,只需
時,只需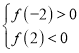 ,即
,即![]() ,解得
,解得![]() ,
,
當![]() 時,令
時,令![]() ,解得
,解得![]() ,
,
所以函數![]() 在區間
在區間![]() 上具有唯一零點
上具有唯一零點![]() ,符合題意,
,符合題意,
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
綜上所述:實數![]() 的取值范圍為
的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖是國家統計局給出的2014年至2018年我國城鄉就業人員數量的統計圖表,結合這張圖表,以下說法錯誤的是( )
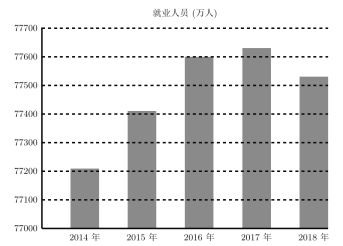
A.2017年就業人員數量是最多的
B.2017年至2018年就業人員數量呈遞減狀態
C.2016年至2017年就業人員數量與前兩年比較,增加速度減緩
D.2018年就業人員數量比2014年就業人員數量增長超過400萬人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國古代數學家劉徽用圓內接正多邊形的面積去逼近圓的面積求圓周率![]() ,他從單位圓內接正六邊形算起,令邊數一倍一倍地增加,即12,24,48,…,192,…,逐個算出正六邊形,正十二邊形,正二十四邊形,…,正一百九十二邊形,…的面積,這些數值逐步地逼近圓面積,劉徽算到了正一百九十二邊形,這時候
,他從單位圓內接正六邊形算起,令邊數一倍一倍地增加,即12,24,48,…,192,…,逐個算出正六邊形,正十二邊形,正二十四邊形,…,正一百九十二邊形,…的面積,這些數值逐步地逼近圓面積,劉徽算到了正一百九十二邊形,這時候![]() 的近似值是3.141024,劉徽稱這個方法為“割圓術”,并且把“割圓術”的特點概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的,用有限來逼近無窮,這種思想極其重要,對后世產生了巨大影響.按照上面“割圓術”,用正二十四邊形來估算圓周率,則
的近似值是3.141024,劉徽稱這個方法為“割圓術”,并且把“割圓術”的特點概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的,用有限來逼近無窮,這種思想極其重要,對后世產生了巨大影響.按照上面“割圓術”,用正二十四邊形來估算圓周率,則![]() 的近似值是( )(精確到
的近似值是( )(精確到![]() ).(參考數據
).(參考數據![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,直線l與橢圓C交于P,Q兩點,且點M滿足
,直線l與橢圓C交于P,Q兩點,且點M滿足![]() .
.
(1)若點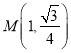 ,求直線
,求直線![]() 的方程;
的方程;
(2)若直線l過點![]() 且不與x軸重合,過點M作垂直于l的直線
且不與x軸重合,過點M作垂直于l的直線![]() 與y軸交于點
與y軸交于點![]() ,求實數t的取值范圍.
,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設中心在原點O,焦點在x軸上的橢圓C過點![]() ,F為C的右焦點,⊙F的方程為
,F為C的右焦點,⊙F的方程為![]()
(1)求C的方程;
(2)若直線![]()
![]() 與⊙O相切,與⊙F交于M、N兩點,與C交于P、Q兩點,其中M、P在第一象限,記⊙O的面積為
與⊙O相切,與⊙F交于M、N兩點,與C交于P、Q兩點,其中M、P在第一象限,記⊙O的面積為![]() ,求
,求![]() 取最大值時,直線l的方程.
取最大值時,直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足:
滿足:![]() ,
,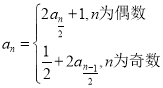 ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)設![]() ,求證:數列
,求證:數列![]() 是等比數列,并求出其通項公式;
是等比數列,并求出其通項公式;
(3)對任意的![]() ,
,![]() ,在數列
,在數列![]() 中是否存在連續的
中是否存在連續的![]() 項構成等差數列?若存在,寫出這
項構成等差數列?若存在,寫出這![]() 項,并證明這
項,并證明這![]() 項構成等差數列:若不存在,請說明理由.
項構成等差數列:若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩城市![]() 和
和![]() 相距
相距![]() ,現計劃在兩城市外以
,現計劃在兩城市外以![]() 為直徑的半圓
為直徑的半圓![]() 上選擇一點
上選擇一點![]() 建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關,對城
建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關,對城![]() 和城
和城![]() 的總影響度為城
的總影響度為城![]() 和城
和城![]() 的影響度之和,記
的影響度之和,記![]() 點到城
點到城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理場對城
處的垃圾處理場對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() ,統計調查表明:垃圾處理場對城
,統計調查表明:垃圾處理場對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數為4,對城
的距離的平方成反比,比例系數為4,對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數為
的距離的平方成反比,比例系數為![]() ,當垃圾處理場建在
,當垃圾處理場建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065;
的總影響度為0.065;
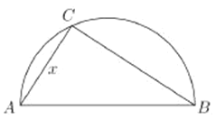
(1)將![]() 表示成
表示成![]() 的函數;
的函數;
(2)判斷![]() 上是否存在一點,使建在此處的垃圾處理場對城
上是否存在一點,使建在此處的垃圾處理場對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,說明理由;
的距離;若不存在,說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)設![]() 是
是![]() 的反函數.當
的反函數.當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 的解集中恰好有一個元素,求實數
的解集中恰好有一個元素,求實數![]() 的值;
的值;
(3)設![]() ,若對任意
,若對任意![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的差不超過
上的最大值與最小值的差不超過![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,若
,若![]() ,則稱
,則稱![]() 是“
是“![]() 數列”.
數列”.
(1)若![]() 是“
是“![]() 數列”,且
數列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 是等差數列,首項為
是等差數列,首項為![]() ,公差為
,公差為![]() ,且
,且![]() ,判斷
,判斷![]() 是否為“
是否為“![]() 數列”;
數列”;
(3)設數列![]() 是等比數列,公比為
是等比數列,公比為![]() ,若數列
,若數列![]() 與
與![]() 都是“
都是“![]() 數列”,求
數列”,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com