【題目】如圖是國家統計局給出的2014年至2018年我國城鄉就業人員數量的統計圖表，結合這張圖表，以下說法錯誤的是（ ）
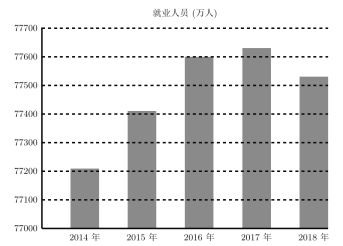
A.2017年就業人員數量是最多的
B.2017年至2018年就業人員數量呈遞減狀態
C.2016年至2017年就業人員數量與前兩年比較，增加速度減緩
D.2018年就業人員數量比2014年就業人員數量增長超過400萬人
學而優銜接教材南京大學出版社系列答案
小學課堂作業系列答案
金博士一點全通系列答案科目：高中數學 來源： 題型：
【題目】如圖1，在等腰梯形
中，兩腰
，底邊
，
，
，
是
的三等分點，
是
的中點.分別沿
，
將四邊形
和
折起，使
，
重合于點
，得到如圖2所示的幾何體.在圖2中，
，
分別為
，
的中點.
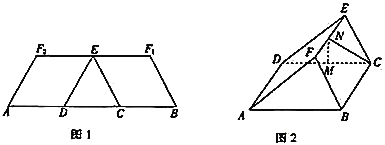
（1）證明：
平面
.
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
：
（
），直線
：
，與交于P、Q兩點，
為P關于y軸的對稱點，直線
與y軸交于點
；
（1）若點
是的一個焦點，求的漸近線方程；
（2）若
，點P的坐標為
，且
，求k的值；
（3）若
，求n關于b的表達式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖:雙曲線
:
的左、右焦點分別為
,
,過作直線
交
軸于點
.
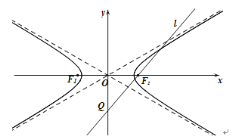
(1)當直線平行于的一條漸近線時,求點到直線的距離;
(2)當直線的斜率為
時,在的右支上是否存在點
,滿足
？若存在,求出點的坐標;若不存在,說明理由;
(3)若直線與交于不同兩點
、
,且上存在一點
,滿足
(其中
為坐標原點),求直線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若數列
對任意的
，都有
，且
，則稱數列為“k級創新數列”.
（1）已知數列
滿足
且
，試判斷數列
是否為“2級創新數列”，并說明理由；
（2）已知正數數列
為“k級創新數列”且
，若
，求數列的前n項積
；
（3）設
，
是方程
的兩個實根
，令
，在（2）的條件下，記數列
的通項
，求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，
，設
的內切圓分別與邊
相切于點
，已知
，記動點
的軌跡為曲線
.
(1)求曲線的方程;
(2)過
的直線與
軸正半軸交于點
，與曲線E交于點
軸，過的另一直線與曲線交于
兩點，若
，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，若在區間
內有且只有一個實數
，使得
成立，則稱函數在區間內具有唯一零點.
（1）判斷函數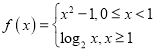
在區間
內是否具有唯一零點，說明理由：
（2）已知向量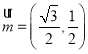
，
，
，證明
在區間
內具有唯一零點.
（3）若函數
在區間
內具有唯一零點，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
