
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)使不等式![]() 對任意
對任意![]() ,
,![]() 恒成立時最大的
恒成立時最大的![]() 記為
記為![]() ,求當(dāng)
,求當(dāng)![]() 時,
時,![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 單調(diào)遞減(2)
單調(diào)遞減(2)![]() (3)
(3)![]()
【解析】
(1)求出函數(shù)的導(dǎo)函數(shù),通過討論![]() 的范圍,求出函數(shù)的單調(diào)區(qū)間即可;
的范圍,求出函數(shù)的單調(diào)區(qū)間即可;
(2)分離變量![]() 得不等式,由恒成立把
得不等式,由恒成立把![]() ,
,![]() 放縮程一個新不等式,再構(gòu)造一個新函數(shù),討論出
放縮程一個新不等式,再構(gòu)造一個新函數(shù),討論出![]() 的范圍,即可得到結(jié)論.
的范圍,即可得到結(jié)論.
(1)因![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
當(dāng)![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 單調(diào)遞減;
單調(diào)遞減;
(2)![]()
![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,
,
令![]() ,
,
由(1)![]() 在
在![]() 上遞增;
上遞增;
(1)當(dāng)![]() ,即
,即![]() 時
時![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上遞增;
上遞增;
∴![]() .
.
(2)當(dāng)![]() ,即
,即![]() 時
時![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上遞減;
上遞減;
∴![]()
![]() .
.
(3)當(dāng)![]() 時,
時,![]() 在上遞增;
在上遞增;
存在唯一實數(shù)![]() ,使得
,使得![]() ,
,
則當(dāng)![]() 時
時![]() .當(dāng)
.當(dāng)![]() 時
時![]() .
.
∴![]() .
.
∴![]() .此時
.此時![]() .
.
令![]() 在
在![]() 上遞增,
上遞增,
![]() ,∴
,∴![]() .
.
綜上所述,![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,
中,![]() ,
,![]() 是曲線段
是曲線段![]() :
:![]() (
(![]() 是參數(shù),
是參數(shù),![]() )的左、右端點,
)的左、右端點,![]() 是
是![]() 上異于
上異于![]() ,
,![]() 的動點,過點
的動點,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() .
.
(1)建立適當(dāng)?shù)臉O坐標(biāo)系,寫出點![]() 軌跡的極坐標(biāo)方程;
軌跡的極坐標(biāo)方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】河北省高考綜合改革從2018年秋季入學(xué)的高一年級學(xué)生開始實施,新高考將實行“3+1+2”模式,其中3表示語文、數(shù)學(xué)、外語三科必選,1表示從物理、歷史兩科中選擇一科,2表示從化學(xué)、生物、政治、地理四科中選擇兩科.某校2018級入學(xué)的高一學(xué)生選科情況如下表:
選科組合 | 物化生 | 物化政 | 物化地 | 物生政 | 物生地 | 物政地 | 史政地 | 史政化 | 史生政 | 史地化 | 史地生 | 史化生 | 合計 |
男 | 130 | 45 | 55 | 30 | 25 | 15 | 30 | 10 | 40 | 10 | 15 | 20 | 425 |
女 | 100 | 45 | 50 | 35 | 35 | 35 | 40 | 20 | 55 | 15 | 25 | 20 | 475 |
合計 | 230 | 90 | 105 | 65 | 60 | 50 | 70 | 30 | 95 | 25 | 40 | 40 | 900 |
(1)完成下面的![]() 列聯(lián)表,并判斷是否在犯錯誤概率不超過0.01的前提下,認(rèn)為“選擇物理與學(xué)生的性別有關(guān)”?
列聯(lián)表,并判斷是否在犯錯誤概率不超過0.01的前提下,認(rèn)為“選擇物理與學(xué)生的性別有關(guān)”?
(2)以頻率估計概率,從該校2018級高一學(xué)生中隨機抽取3名同學(xué),設(shè)這三名同學(xué)中選擇物理的人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
選擇物理 | 不選擇物理 | 合計 | |
男 | 425 | ||
女 | 475 | ||
合計 | 900 |
附表及公式: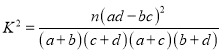
| 0.150 | 0.100 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是國家統(tǒng)計局給出的2014年至2018年我國城鄉(xiāng)就業(yè)人員數(shù)量的統(tǒng)計圖表,結(jié)合這張圖表,以下說法錯誤的是( )
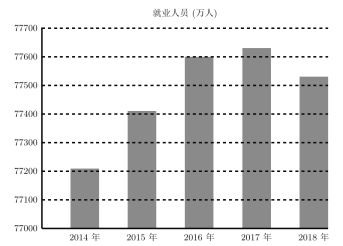
A.2017年就業(yè)人員數(shù)量是最多的
B.2017年至2018年就業(yè)人員數(shù)量呈遞減狀態(tài)
C.2016年至2017年就業(yè)人員數(shù)量與前兩年比較,增加速度減緩
D.2018年就業(yè)人員數(shù)量比2014年就業(yè)人員數(shù)量增長超過400萬人
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 為兩個隨機事件,給出以下命題:(1)若
為兩個隨機事件,給出以下命題:(1)若![]() 為互斥事件,且
為互斥事件,且![]() ,
,![]() ,則
,則![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,則
,則![]() 為相互獨立事件;(3)若
為相互獨立事件;(3)若![]() ,
,![]() ,
,![]() ,則
,則![]() 為相互獨立事件;(4)若
為相互獨立事件;(4)若![]() ,
,![]() ,
,![]() ,則
,則![]() 為相互獨立事件;(5)若
為相互獨立事件;(5)若![]() ,
,![]() ,
,![]() ,則
,則![]() 為相互獨立事件;其中正確命題的個數(shù)為( )
為相互獨立事件;其中正確命題的個數(shù)為( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A′B′C′,∠BAC=90°,AB=AC=λAA′,點M,N分別為A′B和B′C′的中點.
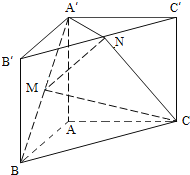
(1)證明:MN∥平面A′ACC′;
(2)若二面角A′﹣MN﹣C為直二面角,求λ的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的一個焦點
)的一個焦點![]() 與拋物線
與拋物線![]() :
:![]() 的焦點重合,且離心率為
的焦點重合,且離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過焦點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 交于
交于![]() ,
,![]() 兩點,滿足
兩點,滿足![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】公元263年左右,我國古代數(shù)學(xué)家劉徽用圓內(nèi)接正多邊形的面積去逼近圓的面積求圓周率![]() ,他從單位圓內(nèi)接正六邊形算起,令邊數(shù)一倍一倍地增加,即12,24,48,…,192,…,逐個算出正六邊形,正十二邊形,正二十四邊形,…,正一百九十二邊形,…的面積,這些數(shù)值逐步地逼近圓面積,劉徽算到了正一百九十二邊形,這時候
,他從單位圓內(nèi)接正六邊形算起,令邊數(shù)一倍一倍地增加,即12,24,48,…,192,…,逐個算出正六邊形,正十二邊形,正二十四邊形,…,正一百九十二邊形,…的面積,這些數(shù)值逐步地逼近圓面積,劉徽算到了正一百九十二邊形,這時候![]() 的近似值是3.141024,劉徽稱這個方法為“割圓術(shù)”,并且把“割圓術(shù)”的特點概括為“割之彌細(xì),所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的,用有限來逼近無窮,這種思想極其重要,對后世產(chǎn)生了巨大影響.按照上面“割圓術(shù)”,用正二十四邊形來估算圓周率,則
的近似值是3.141024,劉徽稱這個方法為“割圓術(shù)”,并且把“割圓術(shù)”的特點概括為“割之彌細(xì),所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的,用有限來逼近無窮,這種思想極其重要,對后世產(chǎn)生了巨大影響.按照上面“割圓術(shù)”,用正二十四邊形來估算圓周率,則![]() 的近似值是( )(精確到
的近似值是( )(精確到![]() ).(參考數(shù)據(jù)
).(參考數(shù)據(jù)![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】兩城市![]() 和
和![]() 相距
相距![]() ,現(xiàn)計劃在兩城市外以
,現(xiàn)計劃在兩城市外以![]() 為直徑的半圓
為直徑的半圓![]() 上選擇一點
上選擇一點![]() 建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關(guān),對城
建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關(guān),對城![]() 和城
和城![]() 的總影響度為城
的總影響度為城![]() 和城
和城![]() 的影響度之和,記
的影響度之和,記![]() 點到城
點到城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理場對城
處的垃圾處理場對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() ,統(tǒng)計調(diào)查表明:垃圾處理場對城
,統(tǒng)計調(diào)查表明:垃圾處理場對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數(shù)為4,對城
的距離的平方成反比,比例系數(shù)為4,對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數(shù)為
的距離的平方成反比,比例系數(shù)為![]() ,當(dāng)垃圾處理場建在
,當(dāng)垃圾處理場建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065;
的總影響度為0.065;
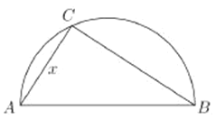
(1)將![]() 表示成
表示成![]() 的函數(shù);
的函數(shù);
(2)判斷![]() 上是否存在一點,使建在此處的垃圾處理場對城
上是否存在一點,使建在此處的垃圾處理場對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,說明理由;
的距離;若不存在,說明理由;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com