【題目】公元263年左右，我國古代數(shù)學(xué)家劉徽用圓內(nèi)接正多邊形的面積去逼近圓的面積求圓周率
，他從單位圓內(nèi)接正六邊形算起，令邊數(shù)一倍一倍地增加，即12，24，48，…，192，…，逐個算出正六邊形，正十二邊形，正二十四邊形，…，正一百九十二邊形，…的面積，這些數(shù)值逐步地逼近圓面積，劉徽算到了正一百九十二邊形，這時候的近似值是3.141024，劉徽稱這個方法為“割圓術(shù)”，并且把“割圓術(shù)”的特點(diǎn)概括為“割之彌細(xì)，所失彌少，割之又割，以至于不可割，則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的，用有限來逼近無窮，這種思想極其重要，對后世產(chǎn)生了巨大影響.按照上面“割圓術(shù)”，用正二十四邊形來估算圓周率，則的近似值是( )（精確到
）.（參考數(shù)據(jù)
）
A.3.14B.3.11C.3.10D.3.05
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知雙曲線
：
（
），直線
：
，與交于P、Q兩點(diǎn)，
為P關(guān)于y軸的對稱點(diǎn)，直線
與y軸交于點(diǎn)
；
（1）若點(diǎn)
是的一個焦點(diǎn)，求的漸近線方程；
（2）若
，點(diǎn)P的坐標(biāo)為
，且
，求k的值；
（3）若
，求n關(guān)于b的表達(dá)式.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，其中
.
（1）求函數(shù)
的單調(diào)區(qū)間；
（2）使不等式
對任意
，
恒成立時最大的
記為
，求當(dāng)
時，
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系中，
，設(shè)
的內(nèi)切圓分別與邊
相切于點(diǎn)
，已知
，記動點(diǎn)
的軌跡為曲線
.
(1)求曲線的方程;
(2)過
的直線與
軸正半軸交于點(diǎn)
，與曲線E交于點(diǎn)
軸，過的另一直線與曲線交于
兩點(diǎn)，若
，求直線
的方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（a＞0）.
（1）求f（x）的單調(diào)增區(qū)間；
（2）當(dāng)x∈[0，π]時，f（x）值域?yàn)?/span>[3，4]，求a，b的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
，曲線
在點(diǎn)
處的切線方程為
.
（Ⅰ）求
，
的值；
（Ⅱ）當(dāng)
時，若
為整數(shù)，且
，求的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】東莞的輕軌給市民出行帶來了很大的方便，越來越多的市民選擇乘坐輕軌出行，很多市民都會開汽車到離家最近的輕軌站，將車停放在輕軌站停車場，然后進(jìn)站乘輕軌出行，這給輕軌站停車場帶來很大的壓力．某輕軌站停車場為了解決這個問題，決定對機(jī)動車停車施行收費(fèi)制度，收費(fèi)標(biāo)準(zhǔn)如下：4小時內(nèi)（含4小時）每輛每次收費(fèi)5元；超過4小時不超過6小時，每增加一小時收費(fèi)增加3元；超過6小時不超過8小時，每增加一小時收費(fèi)增加4元，超過8小時至24小時內(nèi)（含24小時）收費(fèi)30元；超過24小時，按前述標(biāo)準(zhǔn)重新計費(fèi)．上述標(biāo)準(zhǔn)不足一小時的按一小時計費(fèi)．為了調(diào)查該停車場一天的收費(fèi)情況，現(xiàn)統(tǒng)計1000輛車的停留時間（假設(shè)每輛車一天內(nèi)在該停車場僅停車一次），得到下面的頻數(shù)分布表：
|
|
|
|
|
|
|
頻數(shù)（車次） | 100 | 100 | 200 | 200 | 350 | 50 |
以車輛在停車場停留時間位于各區(qū)間的頻率代替車輛在停車場停留時間位于各區(qū)間的概率．
（1）現(xiàn)在用分層抽樣的方法從上面1000輛車中抽取了100輛車進(jìn)行進(jìn)一步深入調(diào)研，記錄并統(tǒng)計了停車時長與司機(jī)性別的
列聯(lián)表：
男 | 女 | 合計 | |
不超過6小時 | 30 | ||
6小時以上 | 20 | ||
合計 | 100 |
完成上述列聯(lián)表，并判斷能否有90%的把握認(rèn)為“停車是否超過6小時”與性別有關(guān)？
（2）（i）
表示某輛車一天之內(nèi)（含一天）在該停車場停車一次所交費(fèi)用，求的概率分布列及期望
；
（ii）現(xiàn)隨機(jī)抽取該停車場內(nèi)停放的3輛車，
表示3輛車中停車費(fèi)用大于的車輛數(shù)，求
的概率．
參考公式：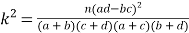
，其中
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，若在區(qū)間
內(nèi)有且只有一個實(shí)數(shù)
，使得
成立，則稱函數(shù)在區(qū)間內(nèi)具有唯一零點(diǎn).
（1）判斷函數(shù)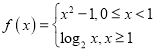
在區(qū)間
內(nèi)是否具有唯一零點(diǎn)，說明理由：
（2）已知向量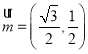
，
，
，證明
在區(qū)間
內(nèi)具有唯一零點(diǎn).
（3）若函數(shù)
在區(qū)間
內(nèi)具有唯一零點(diǎn)，求實(shí)數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】2019年在印度尼西亞日惹舉辦的亞洲乒乓球錦標(biāo)賽男子團(tuán)體決賽中，中國隊(duì)與韓國隊(duì)相遇，中國隊(duì)男子選手A，B，C，D，E依次出場比賽，在以往對戰(zhàn)韓國選手的比賽中他們五人獲勝的概率分別是0.8，0.8，0.8，0.75，0.7，并且比賽勝負(fù)相互獨(dú)立.賽會釆用5局3勝制，先贏3局者獲得勝利.
（1）在決賽中，中國隊(duì)以3∶1獲勝的概率是多少？
（2）求比賽局?jǐn)?shù)的分布列及數(shù)學(xué)期望.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
