
分析 (1)根據函數f(x)=($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$-2,利用向量的運算可得f(x)的解析式,即可求出函數f(x)的單調遞減區間.
(2)根據f(A)=1,求出角A的大小,利用余弦定理求出b,即可求△ABC的面積.
解答 解:(1)向量$\overrightarrow{a}$=(sinx,-1),$\overrightarrow{b}$=$({\sqrt{3}cosx,-\frac{1}{2}})$.
函數f(x)=($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$-2=|$\overrightarrow{a}$|2+$\overrightarrow{a}•\overrightarrow{b}$-2
=sin2x+1+$\sqrt{3}$sinxcosx+$\frac{1}{2}-2$
=$\frac{1}{2}-\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x$-\frac{1}{2}$
=sin(2x-$\frac{π}{6}$),
令$\frac{π}{2}+2kπ≤$2x-$\frac{π}{6}$$≤\frac{3π}{2}+2kπ$,k∈Z.
得:$\frac{π}{3}+kπ$≤x≤$\frac{5π}{6}+kπ$
所以函數f(x)的單調遞減區間為[$\frac{π}{3}+kπ$,$\frac{5π}{6}+kπ$],k∈Z.
(2)由(1)可知f(x)=sin(2x-$\frac{π}{6}$)
那么f(A)═sin(2A-$\frac{π}{6}$)=1
∵$0<A<\frac{π}{2}$,
∴$-\frac{π}{6}<$2A-$\frac{π}{6}$$<\frac{5π}{6}$.
∴2A-$\frac{π}{6}$=$\frac{π}{2}$.
則A=$\frac{π}{3}$.
由余弦定理:a2=b2+c2-2bc•cosA
可得:12=b2+16-4b,
解得:b=2.
∴△ABC的面積S=$\frac{1}{2}$cbsinA=$4\sqrt{3}$.
點評 本題考查了向量的運算和三角函數的化解能力和性質的運用,以及余弦定理的計算.屬于基礎題.


 巧學巧練系列答案
巧學巧練系列答案科目:高中數學 來源: 題型:選擇題
| A. | $({-\frac{{2\sqrt{6}}}{3},\frac{{2\sqrt{6}}}{3}})$ | B. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | C. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | D. | $({-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{3}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$<a<$\frac{3}{2}$ | B. | $\frac{1}{2}$≤a<$\frac{3}{2}$ | C. | $\frac{1}{2}$<a≤$\frac{3}{2}$ | D. | $\frac{1}{2}$≤a≤$\frac{3}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
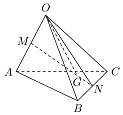 如圖,空間四邊形OABC中,M、N分別是對邊OA、BC的中點,點G在線段MN上,分$\overrightarrow{MN}$所成的定比為2,$\overrightarrow{OG}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,則x、y、z的值分別為$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$.
如圖,空間四邊形OABC中,M、N分別是對邊OA、BC的中點,點G在線段MN上,分$\overrightarrow{MN}$所成的定比為2,$\overrightarrow{OG}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,則x、y、z的值分別為$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
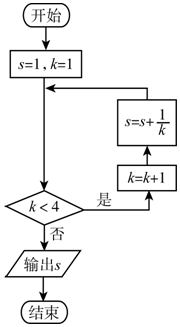
| A. | $\frac{11}{6}$ | B. | $\frac{13}{6}$ | C. | $\frac{25}{12}$ | D. | $\frac{29}{12}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com