
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
分析 根據條件便可求出$|\overrightarrow{AB}|,|\overrightarrow{DC}|$,以及$\overrightarrow{AB}•\overrightarrow{DC}$的值,從而可求出$cos<\overrightarrow{AB},\overrightarrow{DC}>$的值,進而得出異面直線AB與DC所成角θ的大小.
解答 解:$|\overrightarrow{AB}|=\sqrt{20}=2\sqrt{5}$,$|\overrightarrow{DC}|=\sqrt{10}$,$\overrightarrow{AB}•\overrightarrow{DC}=10$;
∴$cos<\overrightarrow{AB},\overrightarrow{DC}>=\frac{10}{2\sqrt{5}×\sqrt{10}}=\frac{\sqrt{2}}{2}$;
∴$<\overrightarrow{AB},\overrightarrow{DC}>=45°$;
∴異面直線AB與DC所成角θ的大小為45°.
故選A.
點評 考查根據向量坐標求向量長度的公式,向量數量積的坐標運算,以及向量夾角余弦的坐標公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
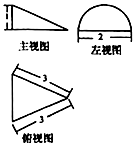
| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 偶函數 | B. | 奇函數 | ||
| C. | 定義域上的增函數 | D. | 定義域上的減函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數,在(-∞,0)上是減函數 | B. | 奇函數,在(-∞,0)上是增函數 | ||
| C. | 偶函數,在(-∞,0)上是減函數 | D. | 偶函數,在(-∞,0)上是增函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
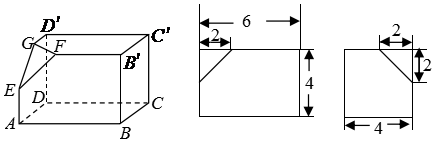
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com