
| A. | $\frac{60}{289}$ | B. | $\frac{90}{289}$ | C. | $\frac{120}{289}$ | D. | $\frac{240}{289}$ |
分析 利用直角三角形三邊與內切圓半徑的關系求出內接正方形邊長,然后分別求出三角形和正方形的面積,根據幾何概型的概率公式即可求出所求
解答 解:由題意,直角三角形兩直角邊長分別為5步和12步,面積為30,設內接正方形邊長為x,則$\frac{x}{12}=\frac{5-x}{5}$,解得x=$\frac{60}{17}$,所以正方形 的面積為$\frac{6{0}^{2}}{1{7}^{2}}$,
∴向此三角形內投豆子,則落在其內接正方形內的概率是$\frac{\frac{6{0}^{2}}{1{7}^{2}}}{30}=\frac{120}{289}$,
故選:C.
點評 本題考查直角三角形內切圓的有關知識,以及幾何概型的概率公式,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 9 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{3}{4}$) | B. | ($\frac{1}{2}$,$\frac{3}{4}$) | C. | (0,$\frac{1}{2}$) | D. | [$\frac{3}{4}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
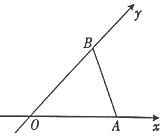 用斜二測畫法畫一個水平放置的平面圖形的直觀圖為如圖所示的等腰三角形,其中OA=OB=1,則原平面圖形的面積為( )
用斜二測畫法畫一個水平放置的平面圖形的直觀圖為如圖所示的等腰三角形,其中OA=OB=1,則原平面圖形的面積為( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | $(0,\frac{1}{2e})$ | C. | $(-∞,0)∪[\frac{1}{2e},+∞)$ | D. | $[\frac{1}{2e},+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 直線 | B. | 橢圓 | C. | 拋物線 | D. | 雙曲線 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com