
| A. | (-∞,0) | B. | $(0,\frac{1}{2e})$ | C. | $(-∞,0)∪[\frac{1}{2e},+∞)$ | D. | $[\frac{1}{2e},+∞)$ |
分析 根據函數與方程的關系將方程進行轉化,利用換元法轉化為方程有解,構造函數求函數的導數,
利用函數極值和單調性的關系進行求解即可
解答 解:由x+a(2x+2m-4ex)[ln(x+m)-lnx]=0得
x+2a(x+m-2ex)ln$\frac{x+m}{x}$=0,
即1+2a($\frac{x+m}{x}$-2e)ln$\frac{x+m}{x}$=0,
即設t=$\frac{x+m}{x}$,則t>0,
則條件等價為1+2a(t-2e)lnt=0,
即(t-2e)lnt=-$\frac{1}{2a}$有解,
設g(t)=(t-2e)lnt,
g′(t)=lnt+1-$\frac{2e}{t}$為增函數,
∵g′(e)=lne+1-$\frac{2e}{e}$=1+1-2=0,
∴當t>e時,g′(t)>0,
當0<t<e時,g′(t)<0,
即當t=e時,函數g(t)取得極小值為:g(e)=(e-2e)lne=-e,
即g(t)≥g(e)=-e,
若(t-2e)lnt=-$\frac{1}{2a}$有解,
則-$\frac{1}{2a}$≥-e,即$\frac{1}{2a}$≤e,
則a<0或a≥$\frac{1}{2e}$,
∴實數a的取值范圍是(-∞,0)∪[$\frac{1}{2e}$,+∞).
故選:C.
點評 本題主要考查了不等式恒成立問題,根據函數與方程的關系,轉化為兩個函數相交問題,利用構造法和導數法求出函數的極值和最值是解題的關鍵.


 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{60}{289}$ | B. | $\frac{90}{289}$ | C. | $\frac{120}{289}$ | D. | $\frac{240}{289}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$i | D. | $\frac{1}{2}$i |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
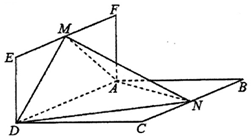 如圖,平面ABCD⊥平面ADEF,四邊形ABCD為菱形,四邊形ADEF為矩形,M,N分別是EF,BC的中點,AB=2AF,∠CBA=
如圖,平面ABCD⊥平面ADEF,四邊形ABCD為菱形,四邊形ADEF為矩形,M,N分別是EF,BC的中點,AB=2AF,∠CBA=查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{4}$-8π | B. | -$\frac{7}{4}$π-8π | C. | -$\frac{π}{4}$-10π | D. | -10π+$\frac{7π}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com