
分析 (1)由Sn=3n2+2n,可得數列{an}是等差數列,可得an=6n-1=bn+bn+1.設等差數列{bn}的公差為d,則$\left\{\begin{array}{l}{{b}_{1}+{b}_{2}=5}\\{{b}_{2}+{b}_{3}=11}\end{array}\right.$,即可得出bn.
(2)cn=$\frac{{{{({a_n}+1)}^{n+1}}}}{{{{({b_n}+2)}^n}}}$=3n×2n+1,利用“錯位相減法”與等比數列的求和公式即可得出.
解答 解:(1)∵Sn=3n2+2n,∴數列{an}是等差數列,首項a1=S1=5,
∵5+a2=3×22+2×2,解得a2=11,
∴公差=11-5=6,∴an=5+6(n-1)=6n-1.∴6n-1=bn+bn+1.
設等差數列{bn}的公差為d,則$\left\{\begin{array}{l}{{b}_{1}+{b}_{2}=5}\\{{b}_{2}+{b}_{3}=11}\end{array}\right.$,
∴2d=11-5=6,解得d=3,∴2b1+3=5,解得b1=1.
∴bn=1+3(n-1)=3n-2.
(2)cn=$\frac{{{{({a_n}+1)}^{n+1}}}}{{{{({b_n}+2)}^n}}}$=$\frac{(6n-1+1)^{n+1}}{(3n-2+2)^{n}}$=6n×2n=3n×2n+1,
∴{cn}的前n項和Tn=3(22+2×23+3×24+…+n×2n+1).
2Tn=3[23+2×24…+(n-1)×2n+1+n×2n+2],
∴-Tn=3[22+23+…+2n+1-n×2n+2]=$3×(\frac{4({2}^{n}-1)}{2-1}-n×{2}^{n+2})$,
∴Tn=(6n-6)×2n+1+12.
點評 本題考查了“錯位相減法”、等差數列與等比數列的定義通項公式及其求和公式,考查了推理能力與計算能力,屬于中檔題.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
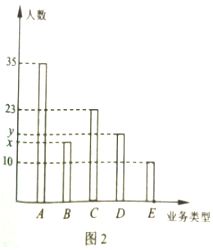 在某天的上午9:00~12:00時段,湛江一間商業銀行隨機收集了100位客戶在營業廳窗口辦理業務類型及用時量的信息,相關數據統計如表1與圖2所示.
在某天的上午9:00~12:00時段,湛江一間商業銀行隨機收集了100位客戶在營業廳窗口辦理業務類型及用時量的信息,相關數據統計如表1與圖2所示.| 一次辦理業務類型 | A型業務 | B型業務 | C型業務 | D型業務 | E型業務 |
| 平均用時量(分鐘/人) | 5 | 6.5 | 8 | 12 | 15 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com