
科目:高中數學 來源: 題型:選擇題
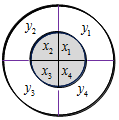 已知兩個半徑不等的圓盤疊放在一起(有一軸穿過它們的圓心),兩圓盤上分別有互相垂直的兩條直徑將其分為四個區域,小圓盤上所寫的實數分別記為x1,x2,x3,x4,大圓盤上所寫的實數分別記為y1,y2,y3,y4,如圖所示.將小圓盤逆時針旋轉i(i=1,2,3,4)次,每次轉動90°,記Ti(i=1,2,3,4)為轉動i次后各區域內兩數乘積之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,則以下結論正確的是( )
已知兩個半徑不等的圓盤疊放在一起(有一軸穿過它們的圓心),兩圓盤上分別有互相垂直的兩條直徑將其分為四個區域,小圓盤上所寫的實數分別記為x1,x2,x3,x4,大圓盤上所寫的實數分別記為y1,y2,y3,y4,如圖所示.將小圓盤逆時針旋轉i(i=1,2,3,4)次,每次轉動90°,記Ti(i=1,2,3,4)為轉動i次后各區域內兩數乘積之和,例如T1=x1y2+x2y3+x3y4+x4y1.若x1+x2+x3+x4<0,y1+y2+y3+y4<0,則以下結論正確的是( )| A. | T1,T2,T3,T4中至少有一個為正數 | B. | T1,T2,T3,T4中至少有一個為負數 | ||
| C. | T1,T2,T3,T4中至多有一個為正數 | D. | T1,T2,T3,T4中至多有一個為負數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 以直角三角形的一直角邊為軸旋轉所得的旋轉體是圓錐 | |
| B. | 以直角梯形的一腰為軸旋轉所得的旋轉體是圓臺 | |
| C. | 有一個面是多邊形,其余各面都是三角形的幾何體叫做棱錐 | |
| D. | 圓錐的側面展開圖為扇形,這個扇形的半徑為圓錐底面圓的半徑 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com