
| A. | (2,+∞) | B. | (-∞,0) | C. | (4,+∞) | D. | (-∞,-2) |
分析 由對數式的真數大于0求出函數的定義域,然后結合復合函數的單調性求得原函數的增區間.
解答 解:由x2-4x>0,得x<0或x>4,
∴函數$f(x)={log_{\frac{1}{2}}}({x^2}-4x)$的定義域為(-∞,0)∪(4,+∞),
當x∈(-∞,0)時,內函數t=x2-4x為減函數,而外函數y=$lo{g}_{\frac{1}{2}}t$為(0,+∞)上的減函數,
∴函數$f(x)={log_{\frac{1}{2}}}({x^2}-4x)$的單調遞增區間是(-∞,0).
故選:B.
點評 本題主要考查了復合函數的單調性以及單調區間的求法.對應復合函數的單調性,一要注意先確定函數的定義域,二要利用復合函數與內層函數和外層函數單調性之間的關系進行判斷,判斷的依據是“同增異減”,是中檔題.


 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{2}{3}π$ | D. | $\frac{{2\sqrt{2}}}{3}π$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4f(1)<f(2) | B. | 4f(1)>f(2) | C. | f(1)<4f(2) | D. | f(1)<2f'(2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
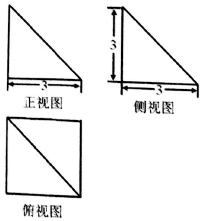
| A. | $\frac{27}{2}π$ | B. | 27π | C. | 27$\sqrt{3}$π | D. | $\frac{27\sqrt{3}π}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com