
| A. | -2017 | B. | -2016 | C. | 2016 | D. | 2017 |
分析 推導出f(x+4)=-f(x+2)=f(x),f(3)=-f(1).從而f(2017)=f(1)=2017,f(f(2017)+2)+1=f(2019)+1=f(3)+1=-f(1)+1,由此能求出結果.
解答 解:∵函數f(x)對任意的x∈R都有f(x+3)=-f(x+1),
∴f(x+4)=-f(x+2)=f(x),f(3)=-f(1).
∵f(1)=2017,
f(2017)=f(1)=2017,
f(f(2017)+2)+1=f(2019)+1=f(3)+1=-f(1)+1=-2017+1=-2016.
故選:B.
點評 本題考查函數值的求不地,是基礎題,解題是要認真審題,注意函數性質的合理運用.


科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$倍 | B. | 2倍 | C. | $\sqrt{2}$倍 | D. | $\frac{3}{2}$倍 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1) | B. | (1)(2) | C. | (1)(2)(4) | D. | (1)(3)(4) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
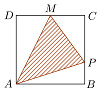 如圖所示,點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A-B-C-M運動時,以點P經過的路程x為自變量,三角形APM的面積為y,函數y=f(x)的圖象大致是( )
如圖所示,點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A-B-C-M運動時,以點P經過的路程x為自變量,三角形APM的面積為y,函數y=f(x)的圖象大致是( )| A. | 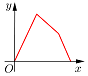 | B. | 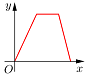 | C. | 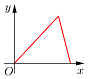 | D. | 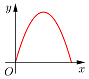 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com