
分析 f(f(a))=2,由此利用分類討論思想能求出a.
解答 解:由f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,f(f(a))=2,
當log2a≤0時,即0<a≤1時,(log2a)2+1=2,
即(log2a)2=1,
解得a=$\frac{1}{2}$,
當log2a>0時,即a>1時,log2(log2a)=2,
解得a=16,
因為a2+1>0,log2(a2+1)=2,即a2+1=4
解得a=$\sqrt{3}$(舍去),或-$\sqrt{3}$,
綜上所述a的值為-$\sqrt{3}$,$\frac{1}{2}$,16,
故答案為:-$\sqrt{3}$,$\frac{1}{2}$,16,
點評 本題考查函數值的求法及應用,是中檔題,解題時要認真審題,注意分段函數的性質的合理運用.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:高中數學 來源: 題型:選擇題
| A. | 12 | B. | 24 | C. | $4\sqrt{3}$ | D. | $8\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
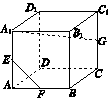 如圖所示,在正方體ABCD-A1B1C1D1中,AA1,AB,CC1的中點分別為E,F,G,則EF與A1G所成的角為( )
如圖所示,在正方體ABCD-A1B1C1D1中,AA1,AB,CC1的中點分別為E,F,G,則EF與A1G所成的角為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=|x| | B. | y=-x3 | C. | y=($\frac{1}{2}$)x | D. | y=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com