
分析 (1)化簡函數的表達式,然后畫出函數的圖象,寫出單調區間即可.
(2)利用函數的圖象,推出實數c的取值范圍.
解答 解:(1)f(x)=|x|(2-x)=$\left\{\begin{array}{l}{2x-{x}^{2},x≥0}\\{{x}^{2}-2x,x<0}\end{array}\right.$,函數的圖象如圖: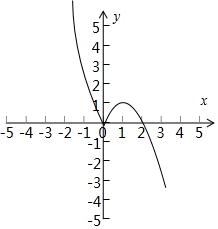
函數的單調增區間(0,1),單調減區間(-∞,0),(1,+∞).
(2)函數f(x)=c恰有三個不同的解,函數在x=1時取得極大值:1,
實數c的取值范圍(0,1).
點評 本題考查分段函數的應用,函數的圖象以及函數的零點個數的判斷,考查數形結合以及計算能力.


 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:選擇題
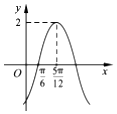 函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,則函數f(x)的解析式為( )
函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,則函數f(x)的解析式為( )| A. | $f(x)=2sin({x-\frac{π}{6}})$ | B. | $f(x)=2sin({2x-\frac{π}{3}})$ | C. | $f(x)=2sin({x+\frac{π}{12}})$ | D. | $f(x)=2sin({2x-\frac{π}{6}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 56 | B. | 68 | C. | 78 | D. | 82 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{4}$] | B. | [0,$\frac{3}{8}$] | C. | ($\frac{1}{4}$,$\frac{1}{2}$] | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com