
 如圖所示,某中學興趣小組設計的自動小車按下面程序運行:
如圖所示,某中學興趣小組設計的自動小車按下面程序運行:分析 (1)由題意得出向下的概率和向右概率,從A過M到B,有兩次向下,再有一次向下與一次向右組合,求得概率值,同理可求海寶過點從A經過N到點C的概率;
(2)求出X=1,2,3時相應的概率,從而可求隨機變量X的分布列及期望.
解答 解:(1)由題意,向下概率為$\frac{1}{3}$,則向右概率為1-$\frac{1}{3}$=$\frac{2}{3}$;
從A過M到B,先有兩次向下,再有一次向下與一次向右組合,
其概率為${(\frac{1}{3})}^{2}$•${C}_{2}^{1}$•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{4}{81}$;
從A過N到C,概率為${C}_{2}^{1}$•$\frac{1}{3}$•$\frac{2}{3}$•${C}_{2}^{1}$•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{16}{81}$;
(2)P(X=1)=($\frac{1}{3}$)3+${C}_{3}^{2}$•($\frac{1}{3}$)2•$\frac{2}{3}$•$\frac{1}{3}$=$\frac{3}{27}$;
P(X=2)=${C}_{4}^{2}$•($\frac{1}{3}$)2•($\frac{2}{3}$)2=$\frac{8}{27}$;
P(X=3)=($\frac{2}{3}$)3+${C}_{3}^{2}$•($\frac{2}{3}$)2•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{16}{27}$,
∴X的分布列為:
| X | 1 | 2 | 3 |
| P | $\frac{3}{27}$ | $\frac{8}{27}$ | $\frac{16}{27}$ |
點評 本題考查了等可能事件的概率以及離散型隨機變量的分布列和數學期望,是中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | $3-\sqrt{3}$ | D. | $3+\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
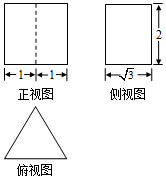
| A. | 12 | B. | 8+2$\sqrt{3}$ | C. | 12+2$\sqrt{3}$ | D. | 12+4$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com